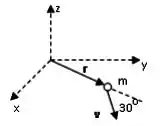
Uma partícula de massa move-se no plano . Em um determinado instante a partícula está a uma distância da origem e sua velocidade tem módulo de e faz um ângulo de com a direção radial (), como mostra a figura. Neste instante, o vetor momento angular da partícula em relação à origem é:
(A) Zero
(B)
(C)
(D)
(E)
Passo 1
O vetor momento angular para uma partícula é dado por:
Ou seja, o produto vetorial do vetor posição com o vetor momento linear .
O momento linear da partícula é dado por:
Então:
Já temos os valores em módulo dos vetores e e o ângulo entre eles , além de um desenho de suas direções. Então, conseguimos resolver esse produto vetorial que achamos o vetor .
Passo 2
Vamos começar com o módulo desse negócio aí.
O módulo do produto vetorial entre dois vetores é dado por:
Sendo o ângulo entre eles.
Então, o módulo do momento angular será:
Substituindo os valores, temos:
Beleza, já sabemos o módulo, mas não podemos sair marcando a resposta antes de saber a direção e o sentido desse vetor.
Passo 3
Primeiro ponto, o produto vetorial entre dois vetores gera um terceiro vetor perpendicular aos outros dois:
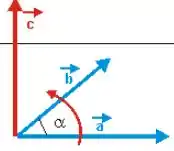
Como os vetores e estão no plano , o vetor estará perpendicular a esse plano, logo, na direção do eixo .
Mas para saber se está no sentido positivo ou negativo da direção , precisamos da regra da mão direita.
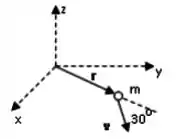
Vamos apontar os nossos dedos indicadores na direção do vetor (nossa palma da mão está virada para o eixo , nesse momento).
Agora, precisamos fechar nossos dedos indicadores no sentido do vetor , para fazer isso, vamos ter que virar nossa mão ao contrário (palma da mão virada para o eixo ).
O sentido do nosso dedão indica a direção do vetor . Como nosso dedão aponta para baixo, o vetor aponta para baixo, tendo direção .
Então, a nossa resposta será:
Ficamos com a letra (C).
Resposta
Letra (C)