Duas partículas, com massas e , estão ligadas por uma haste de massa desprezível e comprimento , conforme indicado na figura abaixo.
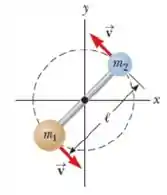
Em um determinado instante de tempo , o sistema começa a girar no plano em torno de um eixo de rotação que passa pelo centro da haste. Sabendo que o momento de inércia do sistema em relação ao eixo de rotação é , quando o módulo da velocidade radial de cada partícula é , o comprimento da haste é dado por:
(a)
(b)
(c)
(d)
(e)
Passo 1
Primeiro ponto importante é que a haste tem massa desprezível, assim, nosso problema apresenta apenas duas partículas pontuais de massas e .
Queremos o comprimento da haste.
Mas como vamos achar isso?
Olhando para o enunciado, temos como dados a velocidade das partículas e o momento de inércia do sistema, além das duas massas e .
OBS: Os dados não necessariamente são valores numéricos. Porém, tratamos como informações conhecidas no problema e assim, podem aparecer na resposta final.
Dá uma olhada nas expressões para o momento angular :
A primeira é para calculada quando temos o momento de inércia de um sistema, já a segunda, é apenas para partículas.
Como temos um sistema de partículas e já sabemos seu momento de inércia , podemos utilizar ambas as expressões.
Então, vamos fazer o seguinte...
Calculamos o momento angular das duas maneiras e depois igualamos essas duas expressões.
Passo 2
A primeira forma é bem direta:
Mas não sabemos quem é , então podemos relacionar isso com a velocidade a partir de:
O raio é a metade do comprimento da haste, então:
Logo, temos:
Substituindo isso em , ficamos com:
Passo 3
Vamos ao cálculo do momento angular com a segunda expressão.
Cada partícula apresenta um momento angular dado por:
Então:
Sendo que, novamente, o raio é metade do comprimento da haste:
Passo 4
Prontinho, podemos igualar os dois e ser feliz:
Cortando , temos:
Logo:
Resposta
Letra (a)