Momento Angular, Rotação, Corpos Rígidos
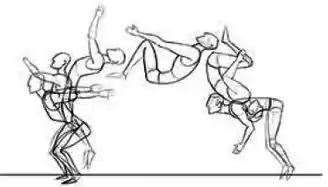
Um ginasta executa um salto mortal. Para isso, enquanto está no ar, dobra o corpo. Podemos dizer que durante sua subida no salto, após perder o contato com o solo, seu momento de inércia em relação ao eixo passando pelo seu centro de massa (perpendicular ao plano do desenho), seu momento angular em relação ao seu centro de massa e sua energia mecânica total, respectivamente,
a) Diminui, se mantém, se mantém.
b) Diminui, se mantém,aumenta.
c) Diminui, diminui, diminui.
d) Aumenta, aumenta, aumenta.
e) Aumenta, diminui, se mantém.
Passo 1
Devemos analisar 3 grandezas nesse movimento, o momento de inércia , o momento angular e a energia mecânica . Bora lá!
Lembrando lá daquele famoso caso da bailarina, quando ela fecha os braços e se encolhe ela gira mais rápido.
O que isso quer nos dizer?
Que a velocidade angular aumenta assim que ela fecha os braços.
Lembrando lá da formula do momento de inércia...
A gente vê que ao aumentar a distância o momento de inércia aumenta. No nosso caso, o ginasta vai estar dobrando o seu corpo, assim o momento de inércia diminui. E como sabemos lá do caso da bailarina, a velocidade angular aumenta, show?
Passo 2
Beleza! A gente sabe que o momento angular se conserva se o torque resultante for nulo. A única força que atua no movimento é o peso, que atua no centro de massa, e por consequência, não gera torque, logo o momento angular se conserva.
Passo 3
Sabemos que o momento de inércia pode ser calculado por:
Como o momento angular se conserva, ao diminuir o , aumenta o , certo? Provando lá o caso da bailarina.
Sabemos que a energia mecânica pode ser calculada por:
Se o ginasta pulasse sem se dobrar, teríamos:
Mas como ele se dobrou, a sua velocidade angular aumentou, ou seja:
E então, a energia mecânica aumenta.
Esquisito, não? haha. Uma galera deve ter marcado que ela se conserva.
Resposta
b) Diminui, se mantém,aumenta.