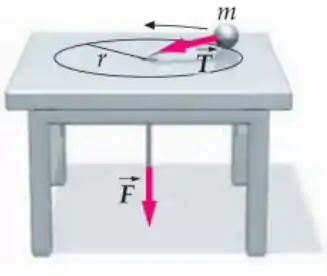
Uma partícula de massa se move com velocidade numa trajetória circular de raio sobre uma mesa sem atrito. A partícula está presa em uma corda que passa por um buraco no centro da mesa como ilustra a figura abaixo. A corda é puxada lentamente para baixo até que a partícula atinja uma distância do buraco e começa a se mover numa nova trajetória circular de raio .
a) Calcule a velocidade final da partícula em função de , e .
b) Calcule a tensão quando a partícula se move numa trajetória circular de raio em termos de e do momento angular .
c) Calcule o trabalho feito pela força de tensão na partícula por integrar . Expresse a resposta em termos de e .
Passo 1
(a) A massa gira gira gira em movimento circular em uma mesa sem atrito, o que podemos dizer do movimento? Sim, isso mesmo, a conservação do momento circular. Isso quer dizer que
Na qual
Então teremos
Implicando que
Passo 2
(b) você acreditaria se eu te disser que no movimento circular a massa acelera? Claro que acreditaria, já estudamos isso, não? Aceleração centrípeta. Assim temos que a tração, que é a força resultante apontada para o centro da mesa pode ser descrita por
Na qual
Nossa aceleração centrípeta. Desta forma
E do passo 1, sabemos que , então
Passo 3
(c) Como o próprio enunciado propõem, mesmo não precisando, precisamos calcular o trabalho realizado pela força de tensão pela integral, ou seja
Os limites de integração nós sabemos né? É o quanto efetivamente nossa massa se moveu, ou seja, . Assim teremos que
Como a massa e o momento é constante, podemos tirar ele pra fora da integral