Duas partículas carregadas, fixas em suas posições, produzem um campo eletrostático nulo em um ponto do espaço. Sobre essa situação, considere as afirmativas abaixo:
- O ponto deve estar necessariamente sobre a linha que passa pelas duas partículas.
- As duas partículas devem ter necessariamente cargas de sinais opostos.
- O potencial eletrostático deve ser necessariamente nulo no ponto .
São VERDADEIRAS as afirmativas:
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
- Nenhuma delas.
Passo 1
Como a questão no diz que o campo eletrostático é nulo, então devemos ter o seguinte:
em que é o campo elétrico gerado pela carga e é o campo produzido pela carga .
A condição mostra para a gente que os campos produzidos pelas cargas têm o mesmo módulo, mesma direção, porém sentidos contrários, ou seja, são vetores anti-paralelos. Como eles têm a mesma direção, isso significa que eles estão ao longo da linha que une as cargas.
Por isso, o item está correto.
Passo 2
Como vimos, os campos elétricos de cada carga devem estar ao longo da mesma linha. Então, vamos considerar a Figura abaixo, em que as cargas estão separadas por uma distância e o ponto está a uma distância de . O vetor unitário está na direção da linha que une as cargas e tem sentido apontando de para .
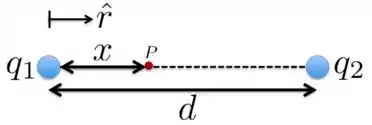
Os campos elétricos produzidos pelas cargas e no ponto acima são, respectivamente, dados por
em que os sinais vão depender dos sinais das cargas.
Fica ligado, porque para , quando for positiva, o campo aponta se afastando de e, por isso, olhando para a Figura acima, vemos que esse campo aponta na direção e sentido de ; se for negativa, então o campo no ponto aponta se aproximando de , por isso na direção e sentido de . Pegou a ideia?
Vamos voltar à nossa primeira condição, que diz . Como eles têm que ser anti-paralelos, se a gente olha para a expressão acima, tiramos que as cargas precisam ter mesmo sinal. Para pegar bem essa ideia, considere que . Então o campo elétrico que essa carga produz é
Como esse vetor aponta para , o vetor também tem que apontar para . Olhando para a expressão de acima, vemos que a carga precisa ser positiva também. Ou seja, e . O mesmo vale se ambas as cargas forem negativas.
Repara aqui numa coisa! Se eu fizer ou (e aí nesse último caso o ponto P estaria à esquerda das cargas) eu poderia ter cargas com sinais diferentes. Por que? Porque nessas regiões o campo elétrico só poderia ser nulo se as cargas tivessem sinais diferentes. Em todo caso, a alternativa está errada porque podemos ter tanto cargas iguais como diferentes.
O item , por essa razão, está incorreto.
Passo 3
O potencial gerado por uma carga pontual é dado por:
Então o potencial no ponto P vai ser:
Esse potencial pode ser positivo, negativo ou nulo, dependendo do sinal das cargas. Ou seja, ele não necessariamente precisa ser nulo.
Por isso, o item também está incorreto.
Resposta
Letra a).