Uma esfera condutora de raio e com carga é envolta por uma camada esférica isolante de raio interno e externo com densidade de carga volumétrica constante.
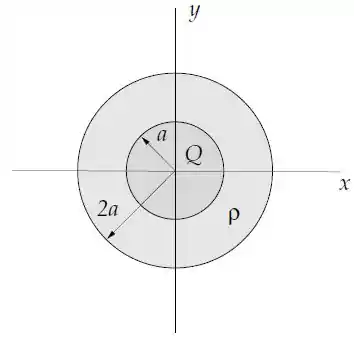
Determine o vetor campo elétrico em todo o espaço;
Determine o potencial elétrico em todo o espaço. Adote potencial nulo no infinito;
Passo 1
Determine o vetor campo elétrico em todo o espaço;
É aquele esquema... viu uma esfera e o cara te pediu o campo elétrico, você pensa logo em Lei de Gauss:
A partir da simetria esférica do problema, já podemos concluir algumas coisas... a primeira delas é que podemos simplificar a Le ide Gauss para:
Outra coisa é que, por causa da sua simetria, o campo elétrico estará sempre na direção radial, logo:
Assim, para qualquer região, teremos apenas que calcular a carga interna e substituir na expressão acima.
Passo 2
Essa região engloba a parte interna da esfera. Como a esfera é condutora, toda a sua carga encontra-se na superfície , logo, quando
Essa região engloba a esfera e parte da casca isolante. Assim, a carga interna aqui será a soma da carga da esfera com a carga de parte da casca esférica.
Para determinar a carga de parte da casca esférica, basta usar a densidade volumétrica de carga:
Portanto, a carga interna total será:
Agora é só substituir na equação do campo elétrico:
Essas regiões intermediárias costumam dar mais trabalho mesmo... relaxa, o resto costuma ser um pouco mais tranquilo.
Essa região engloba a coisa toda. Tínhamos encontrado a seguinte expressão para a carga interna no tópico acima:
A pra calcular a carga interna, basta usar :
Agora é só alegria:
Passo 3
Determine o potencial elétrico em todo o espaço. Adote potencial nulo no infinito;
Por definição, o potencia elétrico é dado por:
Como tanto quanto estão na direção radial, podemos simplesmente escrever:
Então agora o esquema é aplicar isso pra cada região, partindo do infinito. A ideia é sempre começar do infinito até a maior região e, a partir disso, ir usando os resultados anteriores para calcular os potenciais das próximas regiões.
Se liga:
Aqui vamos usar para o caso em que .
Aqui usamos para o caso em que , logo:
Resposta
Resposta
Ei, a resposta está no passo a passo :)