Bem, sabemos que a tensão pode ser dada em relação ao campo elétrico através dessa integral de linha:

No nosso caso, o campo elétrico tem módulo e direção no sentido crescente de como no desenho:

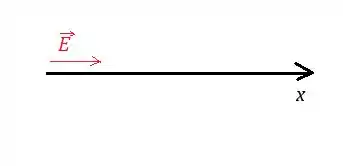
Bem, queremos o valor da tensão em cima do eixo tornando esse eixo o caminho de integração! O então sempre será na direção do eixo crescente:

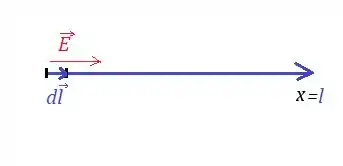
Ora, se o campo elétrico está sempre na direção do eixo assim como o , o produto vetorial dos dois então será:

Só que é só o módulo de (tamanho do vetor) e nesse caso é o mesmo que o trechinho , já que o caminho está em cima do eixo , saca?

Então...