Uma barra isolante fina é posicionada sobre o eixo de um sistema de coordenadas, como mostrado na figura abaixo. O eixo é perpendicular à barra e a origem do sistema coincide com o seu ponto médio. A distribuição de cargas na barra é tal que sua metade à direita está uniformemente carregada com uma densidade linear de carga () e sua metade à esquerda está uniformemente carregada com uma densidade linear de carga . Sobre essa situação, considere as seguintes alternativas:
(I) Para todos os pontos sobre o eixo , o campo elétrico aponta no sentido negativo de .
(II) Para pontos sobre o eixo , é possível determinar a intensidade do campo elétrico conhecendo apenas o potencial elétrico sobre esses pontos.
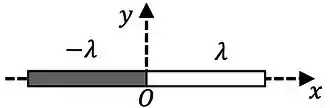
São corretas as alternativas:
(a) Apenas I
(b) Apenas II
(c) Nenhuma delas
(d) Todas elas
Passo 1
Vamos olhar cada uma das frases
I – O eixo passa exatamente no meio da nossa barra. Vamos ver o campo elétrico gerado por um pedacinho da parte esquerda da barra a uma distância da origem e por um pedacinho da barra da parte da direita esquerda também a uma distância da origem.
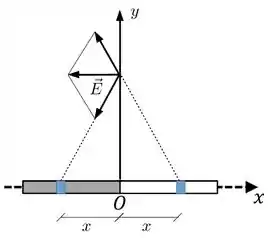
Temos que as componentes verticais dos campos dos dois pedacinhos irão se cancelar, assim sobrando somente uma componente horizontal do campo apontando para a esquerda (sentido negativo de ).
Já que para cada pedaço infinitesimal da parte direita da barra haverá um pedaço na parte esquerda da barra a mesma distância da origem, temos que a soma dos campos das duas barras tem que ser também horizontal apontando para o sentido negativo de . Logo a frase é verdadeira.
II – Vamos lembrar como se relaciona o campo elétrico com o potencial
Ou seja, para sabermos quanto vale o campo em um dado ponto do espaço temos que saber quanto é o gradiente do potencial elétrico nesse ponto e não o valor do potencial nesse ponto!
Só para ilustrar, o potencial que essa barra gera sobre o eixo é . Isso te conta algo sobre o campo? Não! Então essa frase está errada!
Resposta
(a)