Halliday - Vol. 3 – 9º edição – Capítulo 24 – Seção 9 – Exercício 28
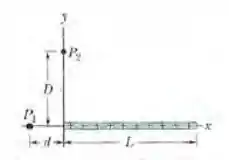
(Capítulo 24.9 – Exercício 28) A Fig. abaixo mostra uma barra fina de plástico que coincide com o eixo x. A barra tem um comprimento L = 12,0 cm e uma carga positiva uniforme Q = 56,1 fC uniformemente distribuída. Com V= 0 no infinito, determine o potencial elétrico no ponto do eixo x, a uma distância d = 2,50 cm de uma das extremidades da barra.
Passo 1
Oiii pessoal, tudo bem? Vamos lá pra mais uma de potencial elétrico
Precisamos calcular o potencial elétrico no ponto do eixo
No caso aí estamos tratando de uma barra então usaremos a equação potencial elétrico aplicado a corpos extensos, mesmo que a barra tenha apenas ela não é uma carga pontual, então temos que ficar ligados.
Vamos aqui também usar o conceito de densidade linear de cargas, já que temos uma barra linear:
Então boraaa
Passo 2
Bem, vamos considerar um pedacinho muito pequeno de barra . Esse pedacinho pequeno, está entre os pontos:
.
Sendo a densidade linear de cargas dessa barra, como ela possui carga uniformemente distribuída:
Diferenciando essa equação, substituindo por , pois queremos que seja a variável para integrar depois na barra toda, obtemos:
Então, o potencial criado por esse pedacinho no ponto é:
Passo 3
Para calcular o potencial da barra toda, e não só de um pedacinho, devemos integrar ao longo de todo o comprimento da barra:
Substituindo os valores dados pelo enunciado:
Sucesso??