Um capacitor esférico é formado por dois condutores em equilíbrio eletrostático. O condutor interno possui formato esférico, de raio , e está carregado com uma carga total . O segundo condutor, de raio interno e raio externo , está carregado com uma carga total .
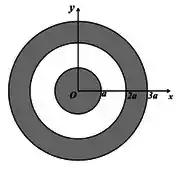
(a) Determine o vetor campo elétrico em todo o espaço e indique como as cargas elétricas estão distribuídas em cada um dos condutores.
(b) Determine o potencial elétrico em todo o espaço. Assuma que o potencial é zero no infinito.
(c) Calcule a capacitância do capacitor.
Passo 1
As cargas elétricas do condutor interno estão localizadas na sua superfície e induzem uma carga negativa de na superfície interna do condutor externo, como pode ser visto na figura abaixo.
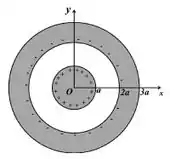
Passo 2
Para calcular o campo elétrico, vamos utilizar a Lei de Gauss, que diz que:
Nas regiões e , o campo elétrico é zero, pois não há cargas no interior dos condutores. Para a região , temos que:
Como o campo aponta das cargas positivas (condutor interno) para as negativas (condutor externo), o vetor pode ser escrito como:
Por fim, para , o campo elétrico é nulo, pois a carga interna total também é nula.
Passo 3
A partir do campo elétrico , obtemos o potencial elétrico por meio da equação:
Para a região , vamos considerar que em um ponto situado no infinito, ou seja, . O potencial em um ponto a uma distância é dado por:
Como , logo, .
Para a região , o potencial será dado por:
Para a região , . Portanto, o potencial será dado por:
Aqui, usamos para o caso em que , ou seja:
Passo 4
A diferença de potencial entre as placas do capacitor é . Logo, utilizando a relação , temos que:
Resposta
(a) , para ; e , para e .
(b) , para ; , para ; e , para .
(c)