Halliday - Vol. 3 – 9º edição – Capítulo 24 – Seção 9 – Exercício 29
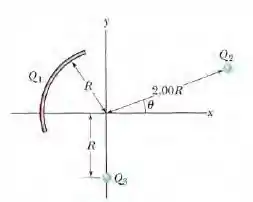
(Capítulo 24.9 – Exercício 29) Na Fig. abaixo, determine o potencial elétrico produzido na origem por um arco de circunferência de carga = +7,21 pC e duas partículas de cargas = 4,00 e = -2,00. O centro de curvatura do arco está na origem, o raio do arco é R = 2,00 m e o ângulo indicado é = 20,0º.
Passo 1
E aí, preparados pra mais uma?
Aqui queremos encontrar o potencial elétrico na origem, ou seja, no ponto
Esse potencial é causado por um arco e duas partículas
Uma característica desse tipo de questão é que esse arco pode ser substituído por uma carga pontual. Isso foi melhor explicado no exercício 24 desse capítulo. Substituindo a barra por uma carga pontual, em que a distância é o raio desse arco de circunferência, temos:
Passo 2
Então, temos
Agora basta a gente substituir os valores dados pelo enunciado e pronto 😊
Note que como o potencial é uma grandeza escalar, o ângulo não foi necessário para desenvolver a questão!
Fechouu