Halliday - Vol. 3 – 9º edição – Capítulo 24 – Seção 9 – Exercício 30
(Cap. 24 – Ex. 30)
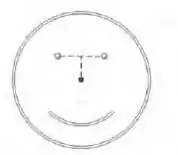
O rosto sorridente da Fig. Abaixo é formado por três elementos:
1: Uma barra fina com uma carga de e a forma de uma circunferência completa com 6,0 cm de raio;
2: Uma segunda barra fina com uma carga de e a forma de um arco de circunferência com de raio, concêntrico com o primeiro elemento, que subtende um ângulo de ;
3: Um dipolo elétrico cujo momento dipolar é perpendicular ao diâmetro da primeira barra que passa pelo ponto médio da segunda barra e cujo módulo é
Determine o potencial elétrico no centro da circunferência.
Passo 1
Faaala galera, coisa mais fofa esse sorrisinho né? Hahahaha o potencial elétrico mais feliz desse livro
Mas vamos lá, queremos encontrar o potencial elétrico no centro da circunferência, que é o nariz do rostinho 😊
Primeiramente, nós devemos lembrar da fórmula do potencial de um dipolo, você lembra? Se não, ela está aqui embaixo:
Como o ângulo que o momento de dipolo faz com o diâmetro da circunferência (que passa pelo centro) é de 90°, basta fazer :
Beleza, esse é o do dipolo, agora precisamos calcular o potencial total
Passo 2
Diferente do campo elétrico, que em questões desse tipo a gente tinha que calcular o vetor campo elétrico, agora nós podemos nos concentrar apenas na distância que esses arcos estão do ponto em que estamos calculando o potencial, que é a origem.
Uma característica desse tipo de questão é que essas barras podem ser substituídas por cargas pontuais. Isso foi melhor explicado no exercício 24 desse capítulo. Substituindo as barras por cargas pontuais, em que a distância é o raio desse arco de circunferência, chamaremos a barra que está em volta da circunferência de e a barra que faz 90° de temos:
Então:
Hehehe no final deu 0
Mas arrasamos!