Uma barra fina e isolante de comprimento é posicionada sobre o eixo de um sistema de coordenadas com seu centro sobre a origem, como mostrado na figura abaixo. Ela possui uma densidade linear de carga estacionária e não-uniforme dada por , onde é uma constante positiva. Considere que o potencial eletrostático é nulo no infinito.

(a) Determine o potencial eletrostático em um ponto sobre um eixo , a uma distância da origem.
(b) Determine o campo eletrostático (módulo, direção e sentido) no mesmo ponto .
(c) Obtenha uma expressão assintótica para o resultado do item (a) no limite . Interprete o resultado
Passo 1
Pra começar, vamos considerar um elemento de comprimento infinitesimal , com coordenada , como na figura abaixo. A distância desse elemento ao ponto é . E sua carga é dada por .
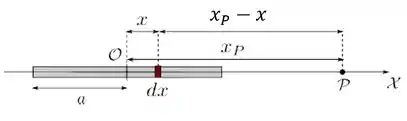
Ele pode ser tratado como uma carga puntiforme e sua contribuição para o potencial eletrostático em é dado por:
Logo, o potencial será dado por:
Para resolver a integral acima, fazemos a substituição: . Temos:
Passo 2
Como as cargas se distribuem apenas ao longo do eixo , as componentes e do campo elétrico devem ser nulas no ponto , ou seja, . A componente pode ser obtida a partir de como:
Logo,
Passo 3
Agora, queremos calcular para . Para começar, vamos olhar para a expansão em série de Taylor da função logaritmo (dada no formulário da prova!):
para .
Logo para pode ser reescrito como:
Substituindo em , temos:
Isso significa que o potencial cai a nesse limite, correspondendo ao de um dipolo elétrico. Isso ocorre porque a carga total da barra é nula, de forma que a contribuição de monopolo está ausente. A barra apresenta uma contribuição de dipolo elétrico, uma vez que ela possui uma concentração de cargas negativas em e positivas em .
Resposta
(a)
(b)
(c)