Um anel circular de raio e uma casca esférica de raios e têm centro comum, situado na origem de um sistema de coordenadas.
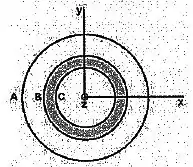
Uma carga total está uniformemente distribuída no anel. Uma carga total está uniformemente distribuída na casca esférica. Sabe-se que e que o anel está contido no plano , conforme mostra o corte da configuração representado na figura acima.
Determine o vetor campo elétrico devido à casca esférica em um ponto arbitrário do eixo tal que .
A partir do resultado do item , determine o potencial elétrico devido à casca esférica no mesmo ponto.
Determine o potencial elétrico devido ao anel no mesmo ponto.
A partir do resultado do item , determine o vetor campo elétrico devido ao anel no mesmo ponto.
Indique, justificando, o sinal do potencial elétrico e o sentido do vetor campo elétrico devidos à configuração total (anel e casca) no ponto arbitrário do eixo tal que .
Passo 1
Determine o vetor campo elétrico devido à casca esférica em um ponto arbitrário do eixo tal que .
Para calcular o campo gerado pela casca esférica, vamos utilizar a Lei de Gauss, dada por:
Devido à simetria do problema, vamos utilizar uma gaussiana esférica de raio igual a . Fazendo isso, a Lei de Gauss pode ser simplificada para:
Obs.: Como estamos calculando o campo gerado apenas pela casca esférica, para o a carga interna consideraremos apenas a carga da casca esférica.
Por fim, como estamos querendo saber o vetor campo elétrico sobre o eixo , teremos:
Passo 2
A partir do resultado do item , determine o potencial elétrico devido à casca esférica no mesmo ponto.
O potencial está relacionado com o campo elétrico através da seguinte equação:
Como estamos calculando uma variação, precisamos de um ponto de referência que, neste caso, costuma ser o infinito , onde , logo:
Finalmente:
Passo 3
Determine o potencial elétrico devido ao anel no mesmo ponto.
Para calcular o potencial gerado pelo anel costumamos começar calculando o potencial gerado por um pedaço infinitesimal do anel, com carga , de forma que:
Onde é a distância entre qualquer ponto do anel ao ponto , sobre o eixo . Assim, podemos escrever a distância como:
Como a carga está uniformemente distribuída no anel, podemos utilizar aqui o conceito de densidade linear de carga, dada por:
Onde corresponde ao tamanho de um pedaço infinitesimal do corpo carregado. Como estamos trabalhando com um anel, , logo:
Assim, voltando à primeira expressão deste passo:
Integrando os dois lados, onde , teremos:
Passo 4
A partir do resultado do item , determine o vetor campo elétrico devido ao anel no mesmo ponto.
Como o potencial elétrico depende somente da distância , podemos encontrar a expressão do campo elétrico a partir da expressão:
Passo 5
Indique, justificando, o sinal do potencial elétrico e o sentido do vetor campo elétrico devidos à configuração total (anel e casca) no ponto arbitrário do eixo tal que .
Potencial elétrico:
O potencial elétrico resultante será a soma dos potenciais individuais da casca esférica e do anel, logo
Substituindo as expressões que encontramos nos Passos 2 e 3, teremos:
Isolando os termos em comum, temos:
Analisando os denominadores:
Assim, o potencial é negativo.
Passo 6
Campo elétrico:
O campo elétrico resultante no ponto será a soma vetorial dos campos individuais da casca esférica e do anel, logo:
Substituindo as expressões que encontramos nos Passos 1 e 4, teremos:
Colocando os termos em comum em evidência, teremos:
Para facilitar a análise, vamos colocar o em evidência também:
Analisando os denominadores:
Logo, o vetor campo elétrico possui o sentido do vetor .
Resposta
O potencial elétrico é negativo e o vetor campo elétrico possui sentido do vetor .