Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Potencial Elétrico Gerado por Corpos Extensos

Ver Teoria
Exercício 661234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

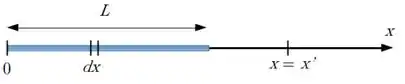
Considere um elemento de carga de comprimento d x situado em uma posição x qualquer da linha, veja a ilustração. Escreva o potencial d V que este elemento produz em x ' , com x ' > L .

(a) Determine o potencial elétrico produzido por toda a linha de carga em x = x ' , com x ' > L .

(b) Use o resultado do item (b) para calcular o campo elétrico em x = x ' .

(c) Suponha que uma carga puntiforme q < 0 esteja em x = x ' . Determine o trabalho mínimo que um agente externo deve realizar para levar a carga para x = ∞ .

Passo 1

O primeiro passo é determinar o potencial d V que d x produz em x ' . Para isso, vamos considerar que d x é uma carga puntiforme com carga d q = Q L d x (aqui já estamos considerando que a carga Q está uniformemente distribuída em L ). A distância r entre a carga d x e o ponto x ' é dada por r = x ' - x . Temos:

d V = 1 4 π ϵ 0 d q r = 1 4 π ϵ 0 L Q x ' - x d x .

Passo 2

Para calcular o potencial elétrico V ( x ' ) , temos que integrar d V ao longo de toda a linha, beleza? Reparem que já escrevi a dependência de x ' em V ( x ' ) porque vamos precisar disso depois.

Bem, vamos lá!

V ( x ' ) = ∫ d V = ∫ 0 L 1 4 π ϵ 0 L Q x ' - x d x ,

V ( x ' ) = Q 4 π ϵ 0 L ∫ 0 L 1 x ' - x d x ,

V ( x ' ) = - Q 4 π ϵ 0 L ln ⁡ x ' - x 0 L = - Q 4 π ϵ 0 L ln ⁡ x ' - L - ln ⁡ x ' ,

V x ' = - Q 4 π ϵ 0 L ln ⁡ x ' - L x ' = - Q 4 π ϵ 0 L ln ⁡ 1 - L x ' .

Passo 3

O campo elétrico E ( x ) pode ser calculado como (lembrem que essa questão só tem uma dimensão e, por isso, vamos calcular o campo elétrico apenas na componente x ):

E ( x ) = - ∂ V x ∂ x .

Aqui tem um detalhe: renomeamos a variável x ' para x !

Continuando:

E ( x ) = Q 4 π ϵ 0 L ∂ ∂ x ln ⁡ 1 - L x ,

E ( x ) = Q 4 π ϵ 0 L L x 2 - L x = Q 4 π ϵ 0 L x 2 - L x .

Passo 4

O trabalho que o agente externo precisa realizar é dado por:

W a → b = - ( U b - U a ) ,

onde vamos considerar que b é o ponto no infinito e a = x ' .

Como U = q V , U ∞ = q V ∞ = - q V ∞ e U x ' = q V x ' = - q V x ' , já que q < 0 . Aqui, vamos adotar V ∞ = 0 .

Passo 5

Substituindo os valores de U ∞ = 0 e U x ' = - q V x ' em W x ' → ∞ , chegamos em:

W x ' → ∞ = - q V x ' ,

W x ' → ∞ = q Q 4 π ϵ 0 L ln ⁡ 1 - L x ' .

Resposta

(a) O potencial elétrico é dado por:

V x ' = - Q 4 π ϵ 0 L ln ⁡ 1 - L x ' .

(b) O campo elétrico em x = x ' é dado por:

E ( x ' ) = Q 4 π ϵ 0 L x ' 2 - L x ' .

(c) O trabalho mínimo que um agente externo deve realizar para levar a carga para x = ∞ é dado por:

W x ' → ∞ = q Q 4 π ϵ 0 L ln ⁡ 1 - L x ' .

Exercícios de Livros Relacionados

Uma barra de plástico tem a forma de um circunferência de raio R = 8,20 cm. A barra possui uma carga Q 1 = +4,20 pC uniformemente distribuída ao longo de um quarto de circunferência e uma carga Q 2 =
A Fig. abaixo mostra uma barra fina de plástico que coincide com o eixo x. A barra tem um comprimento L = 12,0 cm e uma carga positiva uniforme Q = 56,1 fC uniformemente distribuída. Com V= 0 no infin
O rosto sorridente da Fig. Abaixo é formado por três elementos: 1: Uma barra fina com uma carga de -3,0μ C e a forma de uma circunferência completa com 6,0c m de raio; 2: Uma segunda barra fina com um
Qual é o módulo do campo elétrico no ponto 3,00 i ^ - 2,00 j ^ + 4,00 k ^ m se o potencial elétrico é dado por V = 2 x y z 2 , em que V está em volts e x, y e z estão em metros?
Um elétron é colocado no plano xy, onde o potencial elétrico varia com x e y de acordo com os gráficos da figura abaixo (o potencial não depende de z) . Em termos dos vetores unitários, qual é a força