Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Potencial Elétrico Gerado por Corpos Extensos

Ver Teoria
Exercício 812345679101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

a ) Considere um disco de raio a carregado uniformemente com carga Q . Calcule o potencial elétrico ao longo do eixo a uma distancia x do centro do disco. Adote potencial nulo no infinito.

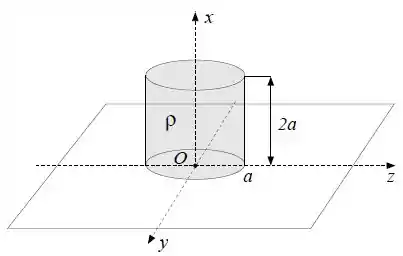
b ) Calcule o potencial elétrico no ponto O com coordenadas x = y = z = 0 devido a um cilindro de altura 2 a e raio de base a , uniformemente carregado com densidade volumétrica de carga ρ . A base do cilindro está contida no plano y z e seu eixo coincide com o eixo x , conforme a figura. Sugestão: Decomponha o cilindro em discos elementares de altura d x e utilize o resultado do item (a).

Passo 1

a ) Considere um disco de raio a carregado uniformemente com carga Q . Calcule o potencial elétrico ao longo do eixo a uma distancia x do centro do disco. Adote potencial nulo no infinito.

Vamos começar calculando o potencial d V de um elemento infinitesimal do disco.

d V = 1 4 π ϵ 0 d q x 2 + r 2

Vamos aproveitar a simetria cilíndrica do problema e dizer que esses elementos infinitesimais de carga d q são anéis muito finos. Assim, podemos dizer que:

d q = σ 2 π r   d r = Q π a 2 2 π r   d r

d q = 2 Q a 2   r   d r

0 < r < a

Agora já podemos calcular o potencial. Substituindo isso na expressão de d V , arrumando e integrando esse cara, temos o seguinte:

V = 2 Q 4 π ϵ 0 a 2 ∫ 0 a r x 2 + r 2 d r

Não tem motivo pra ficar nervoso... essa é uma integral que costuma aparecer bastante, então a resposta dela provavelmente está no formulário da prova.

V = 2 Q 4 π ϵ 0 a 2 x 2 + r 2 0 a

V = 2 Q 4 π ϵ 0 a 2 x 2 + a 2 - a

V = Q 2 π ϵ 0 a 2 x 2 + a 2 - a

Passo 2

b ) Calcule o potencial elétrico no ponto O com coordenadas x = y = z = 0 devido a um cilindro de altura 2 a e raio de base a , uniformemente carregado com densidade volumétrica de carga ρ . A base do cilindro está contida no plano y z e seu eixo coincide com o eixo x , conforme a figura. Sugestão: Decomponha o cilindro em discos elementares de altura d x e utilize o resultado do item (a).

Decompondo o cilindro em discos de altura d x e carga d q , o seu potencial d V pode ser escrito como:

d V = d q 2 π ϵ 0 a 2 x 2 + a 2 - x  

Como o cilindro possui densidade volumétrica de carga ρ , podemos usar essa densidade para encontrar uma expressão para d q :

d q = ρ   d V o l = ρ π a 2 d x

Para descobrir o potencial total do cilindro no ponto O , temos agora apenas que integrar esse cara:

V O = ρ π a 2 2 π ϵ 0 a 2 ∫ 0 2 a x 2 + a 2 - x d x = ρ 2 ϵ 0 ∫ 0 2 a x 2 + a 2 - x d x

Essa integral que aparece agora:

∫ x 2 + a 2 d x

É outra integral dessas que você olha, fica nervoso, mas antes de surtar, tem que dar uma olhada no formulário pra ver se a integral está por lá, beleza?

Voltando ao problema:

V O = ρ 2 ϵ 0 x x 2 + a 2 2 + a 2 2 ln ⁡ x + x 2 + a 2 - x 2 2 0 2 a

Substituindo os valores:

V O = ρ 2 ϵ 0 2 a 4 a 2 + a 2 2 + a 2 2 ln ⁡ 2 a + 2 a 2 + a 2 - 2 a 2 2 - 0 + a 2 2 ln ⁡ a - 0

V O = ρ a 2 2 ϵ 0 5 + 1 2 ln ⁡ a 2 + 5 - 2 - 1 2 ln ⁡ a

E finalmente!

V O = ρ a 2 2 ϵ 0 5 - 2 + 1 2 ln ⁡ 2 + 5

Resposta

a )

V = Q 2 π ϵ 0 a 2 x 2 + a 2 - a

b )

V O = ρ a 2 2 ϵ 0 5 - 2 + 1 2 ln ⁡ 2 + 5

Exercícios de Livros Relacionados

Uma barra de plástico tem a forma de um circunferência de raio R = 8,20 cm. A barra possui uma carga Q 1 = +4,20 pC uniformemente distribuída ao longo de um quarto de circunferência e uma carga Q 2 =
A Fig. abaixo mostra uma barra fina de plástico que coincide com o eixo x. A barra tem um comprimento L = 12,0 cm e uma carga positiva uniforme Q = 56,1 fC uniformemente distribuída. Com V= 0 no infin
O rosto sorridente da Fig. Abaixo é formado por três elementos: 1: Uma barra fina com uma carga de -3,0μ C e a forma de uma circunferência completa com 6,0c m de raio; 2: Uma segunda barra fina com um
Qual é o módulo do campo elétrico no ponto 3,00 i ^ - 2,00 j ^ + 4,00 k ^ m se o potencial elétrico é dado por V = 2 x y z 2 , em que V está em volts e x, y e z estão em metros?
Um elétron é colocado no plano xy, onde o potencial elétrico varia com x e y de acordo com os gráficos da figura abaixo (o potencial não depende de z) . Em termos dos vetores unitários, qual é a força