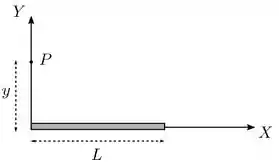
Uma barra isolante fina de comprimento é posicionada sobre o eixo de um sistema de coordenadas, como mostrado na figura abaixo. Suas extremidades estão nos pontos e . Ela encontra-se carregada com uma densidade linear de carga estacionária, mas não-uniforme dada por , onde e uma constante positiva.
(a) Determine a carga total contida na barra.
(b) Determine o potencial elétrico produzido pela barra em um ponto sobre o eixo , localizado a uma distância acima da extremidade esquerda da barra. Considere que o potencial é nulo em um ponto infinitamente afastado da barra.
(c) A componente do campo elétrico no ponto pode ser obtida a partir do potencial obtido no item anterior? Justifique.
Passo 1
a) Vamo lá, nesse primeiro item a gente quer saber qual é a carga total da barra.
Pra isso, vamos pegar um elemento infinitesimal com carga , esse elemento estará a uma distância da extremidade esquerda da barra. Como temos uma densidade de cargas na barra, a gente sabe que .
Então a carga da barra vai ser
Passo 2
b) Vamos começar relacionando o elemento de carga (aquele do item anterior) ao ponto . Fazendo Pitágoras, a gente sabe que a distância entre esses dois caras é .
A contribuição do elemento no potencial elétrico é
Então, pra encontrarmos o potencial no ponto , vamos integrar o
O resultado dessa integral cabeluda foi dado no formulário da prova, ela vai ficar assim
Passo 3
c) Não é possível calcularmos a partir de do item anterior. Repare que a expressão de contém apenas relações a pontos do eixo , ou seja, a gente não consegue analisar como o potencial varia de acordo com e consequentemente não é possível estudar a variação de a partir de .
Resposta
- Não é possível calcularmos a partir de do item anterior. Repare que a expressão de contém apenas relações a pontos do eixo , ou seja, a gente não consegue analisar como o potencial varia de acordo com e consequentemente não é possível estudar a variação de a partir de .