Um semianel fino, de raio é posicionado sobre os dois primeiros quadrantes do plano de um sistema de coordenadas com seu centro sobre a origem, como indicado na figura abaixo. Ele está carregado com uma densidade linear de carga não-uniforme dada por , onde é uma constante positiva e é o ângulo polar, medido a partir do eixo .

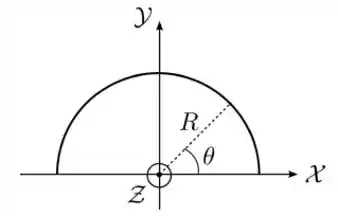
1. Determine a carga total contida no semianel.
2. Determine o potencial elétrico produzido pelo semianel em seu centro, considerando que o potencial é nulo em pontos infinitamente afastados do centro.
3. Determine o campo elétrico (módulo, direção e sentido) produzido pelo semianel no mesmo ponto.

b) O potencial elétrico produzido por no centro do semicírculo é

Integrando essa expressão

c) Para o cálculo do campo elétrico, vamos considerar a figura abaixo, em que temos dois elementos infinitesimais de carga e ’ simétricos, nas posições em que os ângulos são e , respectivamente.

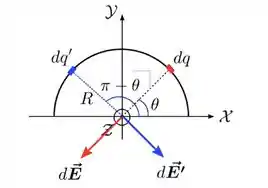
Como a distribuição de cargas depende da função seno, então os dois elementos de carga têm o mesmo módulo, já que e, consequentemente, produzem um campo elétrico no centro do semicírculo que tem o mesmo módulo dado por

Por simetria, como esses campos têm o mesmo módulo, vemos que o campo resultante não terá componente ao longo da direção e podemos apenas olhar para as suas componentes ao longo de . Com isso, o vetor campo infinitesimal resultante pode ser escrito como

Como e , teremos

Integrando, vamos obter que:

ou,