A figura 3 ilustra uma barra não-condutora unidimensional, de comprimento , posicionada ao longo do eixo .
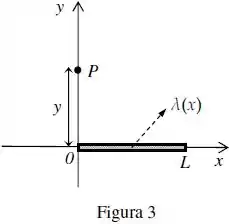
A barra tem uma densidade linear de carga variável , onde é uma constante positiva e . O ponto indicado na figura 3 está localizado ao longo do eixo vertical, a uma distância da origem do sistema de coordenadas.
Admita que o potencial elétrico é nulo no infinito. Para tais circunstâncias:
Calcule o potencial elétrico no ponto .
Calcule a componente do campo elétrico no ponto .
A componente do campo elétrico no ponto pode ser calculada usando o resultado do item (a)? Justifique sua resposta.
Passo 1
Calcule o potencial elétrico no ponto .
O primeiro passo para calcular o potencial é começar com a expressão do potencial gerado por uma pedaço da barra, com carga :
Onde:
Logo:
Agora basta integrar esse cara:
Passo 2
Vamos resolver essa integral utilizando uma substituição simples:
Assim, teremos:
Passo 3
Calcule a componente do campo elétrico no ponto .
O campo elétrico está relacionado ao potencial elétrico através da seguinte equação:
Como o potencial elétrico não depende nem de e nem de , teremos:
Substituindo a expressão do potencial, teremos:
Passo 4
A componente do campo elétrico no ponto pode ser calculada usando o resultado do item (a)? Justifique sua resposta.
Como a expressão do potencial elétrico depende somente da coordenada , só é possível calcular a componente do campo elétrico . A componente do campo elétrico , embora seja diferente de zero, não pode ser calculada utilizando-se o mesmo método.
Resposta
Como a expressão do potencial elétrico depende somente da coordenada , só é possível calcular a componente do campo elétrico . A componente do campo elétrico , embora seja diferente de zero, não pode ser calculada utilizando-se o mesmo método.