Uma barra semicircular de comprimento é composta de três segmentos não-condutores de mesmo comprimento. O segmento do meio é eletricamente neutro e os segmentos das extremidades têm uma carga negativa uniformemente distribuída.
Determine:
O vetor campo elétrico no centro do arco semicircular;
O potencial elétrico total nesse ponto;
A máxima velocidade que um elétron pode adquirir quando este é solto a partir do repouso no centro da barra semicircular.
Passo 1
O vetor campo elétrico no centro do arco semicircular;
Graficamente, a ideia é a seguinte:
Pra começar, vamos explorar a simetria do problema, pegando 2 pontos (com cargas infinitesimais ) simétricos nos arcos carregados negativamente e analisando o campo elétrico gerado por eles no centro do arco:
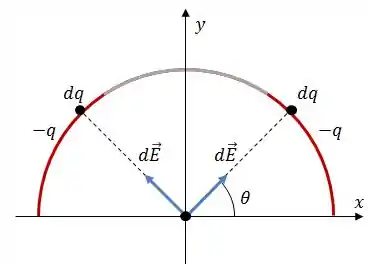
Repara, que esses vetores infinitesimais de campo elétrico apontam para as barras circulares, isso acontece, pois as barras estão carregadas negativamente e geram um campo elétrico que apontam para elas.
Se decompormos os vetores , veremos que as componentes horizontais irão se anular, enquanto as componentes verticais irão se somar, assim, o campo resultante no centro do arco pode ser escrito como:
Onde é a componente vertical do campo elétrico gerado por apenas um dos arcos no centro da semicircunferência, e esse cara que vamos encontrar.
Passo 2
Vamos agora calcular o campo , sabemos que ele é a componente vertical do vetor campo elétrico gerado por uma das barras:
Importante ressaltar que a componente vertical do vetor unitário aponta no sentido positivo de , logo, o mesmo pode ser escrito como . Assim:
Onde , pois aqui estamos avaliando apenas uma das barras e a barra faz um ângulo que vai de 0 até um terço de 180º, isso é, .
Como a carga está uniformemente distribuída no arco, podemos utilizar o conceito de densidade linear de carga, dada por:
Aqui não precisamos nos preocupar com o sinal da carga, isso já foi levado em consideração quando assumimos a direção do nosso vetor campo elétrico, agora estamos interessados em encontrar o módulo desse vetor!
Continuando...
Além disso, a distância entre qualquer ponto do arco e o centro do mesmo é , logo . Dessa forma:
Assim, o campo resultante será:
Passo 3
O potencial elétrico total nesse ponto;
Vamos fazer aqui uma análise bem semelhante ao que fizemos na letra . Como os dois arcos são iguais, os potenciais elétricos gerados pelos mesmos também serão os mesmos, dessa forma, o potencial total será:
Onde é o potencial gerado por cada arco, dado por
Fazendo as mesmas substituições que fizemos na letra , teremos:
Assim:
Finalmente, o potencial elétrico total será:
Passo 4
A máxima velocidade que um elétron pode adquirir quando este é solto a partir do repouso no centro da barra semicircular.
A máxima velocidade que o elétron pode adquirir será dada se toda a energia potencial elétrica no centro da semicircunferência for convertida em energia cinética, logo:
Resposta