Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Potencial Elétrico Gerado por Corpos Extensos

Ver Teoria
Exercício 331234567891011121314151617181920212223242526272829303132343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

USP-P1-2012-3

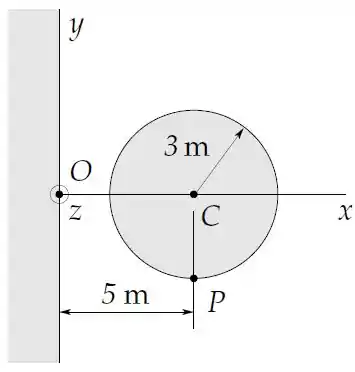
O eixo de um cilindro condutor de 3   m e t r o s de raio dista 5   m e t r o s do plano y z conforme a figura. O cilindro é infinito na direção z perpendicular ao plano da figura e todo o semiespaço x ≤ 0 é preenchido com um material condutor.

O potencial eletrostático num ponto de coordenadas ( x ,   y ,   z ) no espaço fora dos condutores é dado por

V x , y , z = 100 ln ⁡ x + 4 2 + y 2 x - 4 2 + y 2   v o l t s ,

onde x ,   y e z são em metros.

a ) Determine o potencial no ponto C do eixo do cilindro condutor x = 5   m ,   y = z = 0   m .

b ) Determine o vetor campo elétrico em todo o espaço, inclusive no interior dos condutores.

c ) Determine a densidade superficial de carga no ponto O do plano x = y = z = 0 m , e no ponto P x = 5 m ,   y = - 3   m ,   z = 0   m do cilindro. Adote ϵ 0 = 9 × 10 - 12   F / m .

Passo 1

a ) Determine o potencial no ponto C do eixo do cilindro condutor x = 5   m ,   y = z = 0   m .

O potencial que o exercício nos deu é

V x , y , z = 100 ln ⁡ x + 4 2 + y 2 x - 4 2 + y 2  

Só que esse potencial só serve pra região FORA dos condutores!

Mas tem um macete aqui! Lembra que o potencial dentro de condutores tem que ser constante (já que o campo elétrico no seu interior é nulo)? Então isso significa que o potencial na borda do cilindro é igual ao potencial no seu centro, ou seja

V P = V C

Então pra calcular o potencial no centro do cilindro, basta calcular o potencial no ponto P .

Olhando a figura as coordenadas do ponto P são ( 5 ,   - 3 ) . Substituindo essas coordenadas no potencial temos

V P = 100 ln ⁡ 5 + 4 2 + - 3 2 5 - 4 2 + - 3 2 = 100 ln ⁡ 9 2 + 9 1 2 + 9 = 100 ln ⁡ 9 0 10 = 100 ln ⁡ 9 = 200 ln ⁡ 3

Assim o potencial no ponto C será

V C = 2 00 ln ⁡ 3   v o l t s

Passo 2

b ) Determine o vetor campo elétrico em todo o espaço, inclusive no interior dos condutores.

Por definição:

E = - d V d r

Onde:

V x , y , z = 100 ln ⁡ x + 4 2 + y 2 x - 4 2 + y 2

Pra descobrir cada componente do campo elétrico, temos que derivar parcialmente V em função de cada uma das coordenadas x ,   y e z .

E x = - ∂ V ∂ x = - 200 x + 4 x + 4 2 + y 2 - x - 4 x - 4 2 + y 2   ( V / m )

E y = - ∂ V ∂ y = - 200 y x + 4 2 + y 2 - y x - 4 2 + y 2   ( V / m )

E z = - ∂ V ∂ z = 0

Por fim, o problema pede pra calcular também o campo no interior dos condutores... aí tem um detalhe que você jamais pode esquecer: o campo elétrico no interior de um condutor é sempre nulo!

Passo 3

c ) Determine a densidade superficial de carga no ponto O do plano x = y = z = 0 m , e no ponto P x = 5 m ,   y = - 3   m ,   z = 0   m do cilindro. Adote ϵ 0 = 9 × 10 - 12   F / m .

Pra fazer esse item temos que saber como é o campo elétrico produzido pelos dois condutores.

Chamando a densidade superficial de carga do condutor da região x ≤ 0 de σ P e desenhando uma gaussiana como a figura abaixo

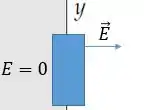
Se a área dentro dessa gaussiana é A temos pela lei de Gauss que

Φ E = Q ϵ 0

E A = σ P A ϵ 0

E → p l a n o = σ P ϵ 0 x ^

Já para o cilindro vamos desenhar uma gaussiana cilíndrica de raio r maior que o raio R do cilindro ( R = 3 m ) e de comprimento L

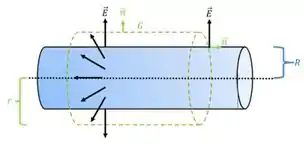
Pela lei de Gauss

Φ E = Q i n ϵ 0

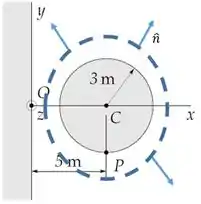
Vamos chamar a densidade superficial de carga do cilindro de σ C

E 2 π r L = σ C 2 π R L ϵ 0

E → c i l i n d t r o = σ C R r ϵ 0 n ^

Onde n ^ é o vetor que aponta pra fora da direção do cilindro

Passo 4

O campo elétrico que descobrimos no item (b) é a soma dos campos do passo anterior. Pra descobrir as densidades de carga basta substituirmos alguns pontos nessas expressões para acharmos algumas relações. Então vamos lá!

Como o campo do cilindro é meio complicado, a gente tem que escolher com cuidado quais pontos do espaço são interessantes para calcular o campo.

Sobre o eixo x entre o cilindro e o campo ( 0 ≤ x ≤ 2 ) o campo do cilindro é

E → c i l i n d t r o = σ C R r ϵ 0 x ^

Num ponto x do eixo x o raio da gaussiana correspondente será r = 5 - x e o raio do cilindro é R = 3 , assim

E → c i l i n d r o = 3 σ C ( 5 - x ) ϵ 0 x ^

Assim o campo resultante será

E → = E → p l a n o + E → c i l i n d r o = σ P ϵ 0 x ^ + 3 σ C 5 - x ϵ 0 x ^

Show! Agora podemos substituir alguns valores!

Olhando o campo do item (b) sobre o eixo x temos que y = 0 , assim a componente x do campo fica

E x = - 200 x + 4 x + 4 2 + y 2 - x - 4 x - 4 2 + y 2 = - 200 x + 4 x + 4 2 + 0 - x - 4 x - 4 2 + 0

E x = - 200 1 x + 4 - 1 x - 4 = - 200 x - 4 - x + 4 x 2 - 4 2 = - 200 - 8 x 2 - 16 = 1600 x 2 - 16

Já as componentes y e z são nulas

E y = - 200 y x + 4 2 + y 2 - y x - 4 2 + y 2 = - 200 0 x + 4 2 + 0 - 0 x - 4 2 + 0 = 0

E z = 0

No ponto x = 0 , temos que

E x = 1600 - 16 = - 100

Por outro lado

E → x = 0 = σ P ϵ 0 x ^ + 3 σ C 5 - x ϵ 0 x ^ = σ P ϵ 0 + 3 σ C 5 ϵ 0 x ^

Assim

σ P ϵ 0 + 3 σ C 5 ϵ 0 = - 100

Já no ponto x = 2

E x = 1600 2 2 - 16 = 1600 4 - 16 = - 400 3

Por outro lado

E → x = 2 = σ P ϵ 0 x ^ + 3 σ C 5 - 2 ϵ 0 x ^ = σ P ϵ 0 + σ C ϵ 0 x ^

Assim

σ P ϵ 0 + σ C ϵ 0 = - 400 3

Passo 5

Agora temos um sisteminha de equações

σ P ϵ 0 + 3 σ C 5 ϵ 0 = - 100

σ P ϵ 0 + σ C ϵ 0 = - 400 3

Subtraindo a primeira da segunda

3 σ C 5 ϵ 0 - σ C ϵ 0 = - 100 + 400 3

- 2 σ C 5 ϵ 0 = 100 3 → σ C = - 500 6 ϵ 0 = - 500 6 × 9 × 10 - 12

σ C = - 7,5 × 10 - 10   C / m 2

Na primeira equação

σ P ϵ 0 = - 100 - 3 σ C 5 ϵ 0 → σ P = - 100 ϵ 0 - 3 5 σ C = - 100 × 9 × 10 - 12 - 3 5 × - 7,5 × 10 - 10

σ P = - 4,5 × 10 - 10   C / m 2

Resposta

a )

V C = 2 00 ln ⁡ 3 V

b )

E x = - 200 x + 4 x + 4 2 + y 2 - x - 4 x - 4 2 + y 2   ( V / m )

E y = - 200 y x + 4 2 + y 2 - y x - 4 2 + y 2   ( V / m )

E z = 0

c )

σ O = - 7,5 × 10 - 10   C / m 2

σ P = - 4 , 5 × 10 - 10   C / m 2

Exercícios de Livros Relacionados

Uma barra de plástico tem a forma de um circunferência de raio R = 8,20 cm. A barra possui uma carga Q 1 = +4,20 pC uniformemente distribuída ao longo de um quarto de circunferência e uma carga Q 2 =
A Fig. abaixo mostra uma barra fina de plástico que coincide com o eixo x. A barra tem um comprimento L = 12,0 cm e uma carga positiva uniforme Q = 56,1 fC uniformemente distribuída. Com V= 0 no infin
O rosto sorridente da Fig. Abaixo é formado por três elementos: 1: Uma barra fina com uma carga de -3,0μ C e a forma de uma circunferência completa com 6,0c m de raio; 2: Uma segunda barra fina com um
Qual é o módulo do campo elétrico no ponto 3,00 i ^ - 2,00 j ^ + 4,00 k ^ m se o potencial elétrico é dado por V = 2 x y z 2 , em que V está em volts e x, y e z estão em metros?
Um elétron é colocado no plano xy, onde o potencial elétrico varia com x e y de acordo com os gráficos da figura abaixo (o potencial não depende de z) . Em termos dos vetores unitários, qual é a força