Densidade de Carga, Potencial Elétrico
A figura mostra uma barra fina de plástico de comprimento , sobre o eixo , carregada com densidade uniforme de carga .
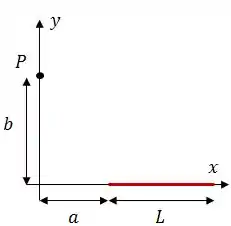
Com no infinito:
Calcule o potencial elétrico no ponto sobre o eixo ;
Determine, a partir do potencial, a componente do campo elétrico em ;
Por que a componente do campo elétrico neste ponto não pode ser calculada usando o resultado do item ?
Dado:
Passo 1
Calcule o potencial elétrico no ponto sobre o eixo ;
Vamos começar escrevendo a expressão do potencial gerado por um pedaço infinitesimal, de carga :
Graficamente, a ideia é essa:
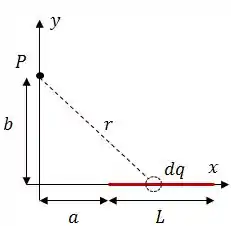
Daqui podemos tirar que:
Substituindo isso na expressão de , teremos:
Passo 2
Pra finalizar, temos apenas que integrar esse cara de até :
Beleza! Essa é daquelas integrais que podem te complicar, mas o próprio problema já te deu a resposta dela.
Logo, continuando:
Passo 3
Determine, a partir do potencial, a componente do campo elétrico em ;
Bom, o potencial em um ponto qualquer sobre o eixo é dado por:
Assim, por definição, o campo elétrico será dado por:
Assim, só temos que derivar esse cara, beleza?
Sim, ficou muito feio isso.
Como ele pediu no ponto P, temos que substituir
Passo 4
Por que a componente do campo elétrico neste ponto não pode ser calculada usando o resultado do item ?
Porque o potencial foi calculado no item para qualquer ponto sobre o eixo , independendo de .
Resposta
Porque o potencial foi calculado no item para qualquer ponto sobre o eixo , independendo de .