A figura abaixo mostra três arcos de circunferência não-condutores de raio .
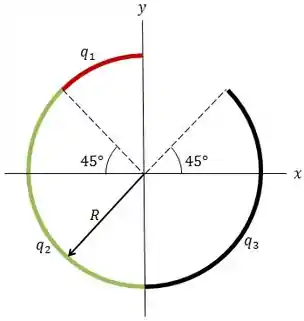
As cargas dos arcos são , e . Com no infinito, qual é o potencial elétrico dos arcos no centro da curvatura?
Passo 1
Como nós possuímos três arcos carregados, o potencial resultante será a soma dos potenciais. Então temos que calcular o potencial de cada um desses arcos.
O fato de serem arcos pode acabar te deixando na dúvida. Mas relaxa, é mais simples do que parece.
Vamos supor que a gente não saiba como resolver o problema e achássemos que íamos ter que pensar na distribuição de carga.
O procedimento aqui consistiria em pegar o potencial de uma carga pontual do corpo no centro e integra-lo no corpo todo. Como essa carga é infinitesimalmente pequena se comparada ao corpo, nós montamos a integral assim:
Assim, como o raio é constante, o potencial de cada arco será dado por:
Portanto:
Viu? Não precisa se preocupar com as distribuições, já que a distância de qualquer elemento infinitesimal para o centro vai ser sempre . Então não tem porque se preocupar.
Vamos adiante.
Passo 2
Como eu falei antes, o potencial resultante será a soma dos potenciais. Sendo assim:
Onde e .
Onde:
;
;
;
Logo: