Seja uma casca esférica não condutora de raio interno e raio externo , veja a figura. A carga total na casca é e está uniformemente distribuída no seu volume. Considere no infinito.
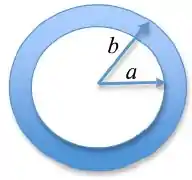
Calcule o módulo do campo elétrico e o potencial elétrico para , onde é a distância de um ponto no espaço ao centro da casca.
Calcule a densidade volumétrica de carga na casca.
Calcule o módulo do campo elétrico para e para .
Calcule o potencial elétrico para e para .
Passo 1
Calcule o módulo do campo elétrico e o potencial elétrico para , onde é a distância de um ponto no espaço ao centro da casca.
Para este tipo de problema costumamos utilizar a Lei de Gauss, dada por:
Nesse caso, como a carga está uniformemente distribuída no volume da casca esférica, podemos nos aproveitar da simetria do problema para simplificar a nossa vida usando uma gaussiana esférica.
Fazendo isso, a integral à esquerda da igualdade pode ser simplificada para:
Onde representa a área da gaussiana que, nesse caso, por se tratar de uma esfera, pode ser escrito como , onde é o raio da nossa gaussiana. Logo:
A variável representa a carga dentro da gaussiana. Aqui, como estamos calculando o campo elétrico para o caso em que , a gaussiana irá englobar toda a casca esférica de carga .
Dessa forma:
Passo 2
Podemos encontrar a expressão para o potencial elétrico utilizando o campo elétrico que encontramos no Passo 1, através da seguinte expressão:
Como essa expressão calcula uma variação de potencial elétrico, para calcularmos o potencial em um ponto específico, precisamos de um valor de referência. Esse valor de referência é geralmente o potencial no infinito, que vale zero. Dessa forma, teremos:
Agora é resolver a integral:
Passo 3
Calcule a densidade volumétrica de carga na casca.
A densidade volumétrica de carga, por definição, é dada por:
Neste problema, como a carga está uniformemente distribuída na casca esférica, a densidade volumétrica de carga pode ser escrita como:
Onde é a carga total da casca e é o seu volume, dado por:
Logo:
Passo 4
Calcule o módulo do campo elétrico para e para .
Vimos no Passo 1 que, por conta da simetria do problema e do fato da carga estar uniformemente distribuída, o campo elétrico pode ser escrito por:
Assim, o nosso trabalho aqui é calcular a carga englobada pela gaussiana em cada caso.
- :
- :
- :
- :
- :
- :
- :
- :
Para esse caso, vamos utilizar a densidade de carga que calculamos no Passo 3 da seguinte forma:
Onde corresponde ao volume da casca esférica englobado pela gaussiana, que vale:
Dessa forma:
Assim, o campo elétrico neste caso será:
Passo 5
Neste caso, a gaussiana não está englobando nenhuma parte casca esférica, logo:
Passo 6
Calcule o potencial elétrico para e para .
Ok, aqui vamos aplicar a relação abaixo que utilizamos no Passo 2 para esses dois casos, beleza?
Vimos no Passo 2 que precisamos de uma referência, um ponto onde saibamos o potencial, certo?
Lá mesmo vimos que o potencial para é dado por:
Assim, para :
Opa, agora que já sabemos o potencial em , podemos aplicar a nossa equação.
Agora é resolver isso aos poucos, beleza?
Pronto! (Por increça que parível)
Passo 7
Show de bola, como agora estamos interessados em pontos em que , vamos adotar como valor de referência o ponto .
Assim, utilizando a expressão que encontramos no Passo 6, teremos:
Utilizando a expressão para o potencial elétrico, e lembrando que para essa região , teremos:
Resposta
Resposta
Ei, a resposta está no passo a passo :)