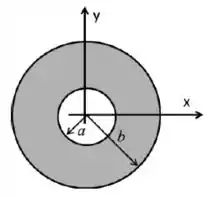
A figura ilustra uma coroa circular disposta no plano , centrada na origem, de raio interno e raio externo . Sua carga está uniformemente distribuída e possui . Use ou .

Considerando a referência para potenciais no infinito, encontre o valor do potencial elétrico num ponto qualquer do eixo , à distância da origem.

Calcule o potencial no ponto e o valor do trabalho realizado pela força eletrostática no deslocamento de uma carga teste desde até o ponto onde o potencial vale .

Suponha que o potencial gerado pela coroa circular no ponto tenha valor . Queremos anular o potencial em , e para isso dispomos de uma carga pontual de valor . Determine todos os pontos do espaço em que podemos posicionar a carga de modo a tornar nulo o potencial em .

Para o ponto em questão, teremos o seguinte potencial:

Para uma carga de prova , o trabalho para leva-la do ponto para o ponto será dado pela seguinte relação:

Como queremos que no ponto , o potencial seja nulo, o potencial gerado pela carga em deve ser igual em módulo ao potencial que já existe, e deve ser negativo para anular o potencial, ou seja:

O potencial gerado por uma carga é dado por:

Onde é a distância do ponto a carga, e é exatamente isso que queremos descobrir. Igualando as duas equações:

Logo, podemos colocar a carga em qualquer ponto do espaço que diste do ponto . Esses pontos formam uma esfera de raio centrada no ponto !