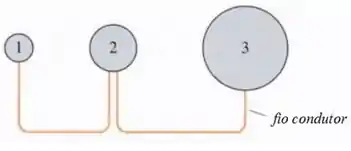
(a)
(b)
(c)
(d)
(e)
Passo 1
O equilíbrio vai ser alcançado quando o potencial elétrico das três esferas for igual. Isso acontece quando:
Como , temos então:
E com isso a gente fica entre as letras (B) e (D) e suas chances de acertar sobem de 20% para 50% ;) rs
Passo 2
Vamos reescrever a igualdade do passo de um jeito mais malandro:
E agora bora escrever cada carga em função de :
E para calcular a densidade de cargas a gente pega isso e divide pela área da esfera:
E aí, como , o contrário vai acontecer com as densidades:
Resposta
Letra (B).
Exercícios de Livros Relacionados
Uma barra de plástico tem a forma de um circunferência de raio R = 8,20 cm. A barra possui uma carga Q 1 = +4,20 pC uniformemente distribuída ao longo de um quarto de circunferência e uma carga Q 2 =
A Fig. abaixo mostra uma barra fina de plástico que coincide com o eixo x. A barra tem um comprimento L = 12,0 cm e uma carga positiva uniforme Q = 56,1 fC uniformemente distribuída. Com V= 0 no infin
O rosto sorridente da Fig. Abaixo é formado por três elementos: 1: Uma barra fina com uma carga de -3,0μ C e a forma de uma circunferência completa com 6,0c m de raio; 2: Uma segunda barra fina com um
Qual é o módulo do campo elétrico no ponto 3,00 i ^ - 2,00 j ^ + 4,00 k ^ m se o potencial elétrico é dado por V = 2 x y z 2 , em que V está em volts e x, y e z estão em metros?
Um elétron é colocado no plano xy, onde o potencial elétrico varia com x e y de acordo com os gráficos da figura abaixo (o potencial não depende de z) . Em termos dos vetores unitários, qual é a força