Um fio de comprimento foi carregado de modo a dotar a metade superior com densidade linear de carga e a metade inferior com densidade linear de carga , onde é uma constante positiva.
- Determine o campo elétrico (módulo, direção e sentido) num ponto situado a uma distância do fio, na direção perpendicular a partir de seu ponto médio.
- Obtenha o potencial elétrico no ponto supracitado.
- Mesmo para grandes distâncias () o campo elétrico não é exatamente nulo. Qual é o comportamento do campo elétrico, como função de , nessa aproximação? Interprete seu resultado
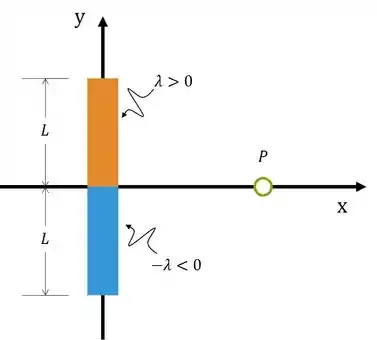
Passo 1
Velha questão de integrar o campo da barra. Como o campo vai ter duas componentes, vamos utilizar um argumento de simetria para não ter que calcular uma delas. Fazendo um esboço do campo em pontos simetricamente opostos:
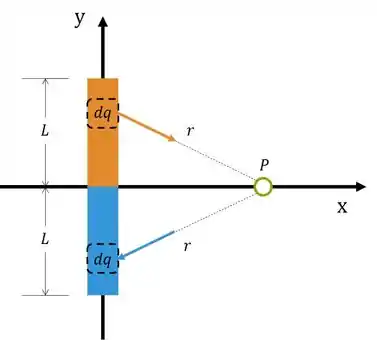
Desse esboço podemos concluir que a componente do campo elétrico em é zero, ao passo que a componente é o dobro de cada uma das barras:
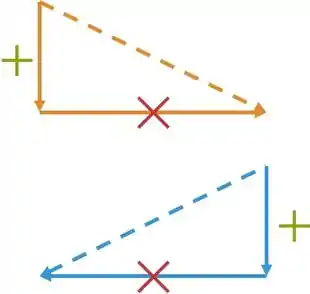
Passo 2
Agora estabelecemos a expressão do campo de uma carga puntiforme:
E a questão se resumo à integrar esse campo em toda a barra:
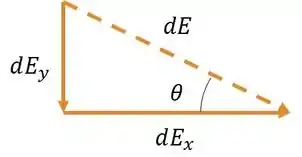
Agora partiu decompor o campo pra podermos seguir com a questão, sendo que à partir desse momento não precisamos nos preocupar com a componente e nem com a barra debaixo, pois é só dobrar o campo. Fazendo pra :
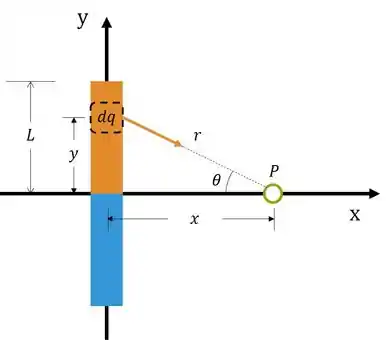
Pela semelhança de triângulos:
Passo 3
Já colocamos o sinal de menos para definir a orientação, pois sabemos que em o campo aponta pra baixo:
Substituindo o valor do seno:
Então temos a integral:
Como o campo é o dobro de uma barra só:
Passo 4
Trocando o diferencial de carga com a definição da densidade:
E substituindo a distância :
Temos:
Arrumando:
Resolvendo por substituição simples:
A integral indefinida fica:
Passo 5
Voltando para e :
Substituindo no campo:
E obtemos nossa expressão:
Portanto para achar o vetor basta multiplicar por :
Passo 6
Agora vamos obter o potencial elétrico das duas maneiras possíveis. Primeiramente integrando o , temos:
Como são duas densidades diferentes, são duas expressões para o potencial:
Arrumando:
Como é o caso da distância de pro ponto ser a mesma de , a função é par, logo:
Ou seja, em qualquer ponto do eixo teremos potencial zero. Se fosse o caso de existir uma barra só ao invés de duas, teríamos a integral:
Que é uma integral medonha que resulta em:
Reze pra não cair na sua prova.
Passo 7
Alternativamente, outro jeito um pouco mais fácil de resolver é pela fórmula da diferença de potencial:
Escolhendo um caminho ao longo de partindo do infinito temos:
Note que se partir do infinito o vetor aponta da direita pra esquerda, por isso o
Ao passo que o campo é:
Logo:
Agora cuidado, o mais importante é você resolver o produto escalar primeiro. Pra sair do produto escalar os módulos não são relevantes, basta analisar os vetores que dão as direções. Neste caso e :
Logo, esse produto escalar zera tudo:
Show? = ]
Passo 8
Finalmente vamos brincar de Séries de Taylor. Zoeira esta questão, porque eles não deram a fórmula:
Ou seja, se for muito menor que é válida a aproximação acima. Agora temos que manipular os dados pra poder substituir essa fórmula aí. O enunciado nos dá:
Ou seja, dividindo por em ambos os lados vamos tentar forçar algo parecido com :
Passo 9
Agora manipulamos a equação do campo:
Dentro da raiz vamos forçar aparecer o :
Passo 10
Substituímos e colocamos o módulo de em evidência:
Agora vamos usar a aproximação do Taylor sendo , pois temos que:
Passo 11
Substituindo de volta:
Se tratarmos de somente:
E é isso aí. Faltou analisar. E aí, como faz? Bom, a análise do gabarito está muito além do que uma pessoa normal conseguiria fazer sozinha. O macete neste caso é olhar por alto a configuração das cargas e ver com o que essa coisa é mais parecida.
São duas barras de mesmo comprimento e com cargas opostas, logo o que mais se assemelha com isso na nossa Fauna eletromagnética é o dipolo elétrico. Justo? Na prova você diria isto e, provavelmente, ganharia todos os pontos. Não teria sentido investigarmos além disso para a nossa análise pois é esforço demais para uma questão improvável de cair, valendo poucos pontos, e que na hora da prova você mal vai lembrar. O truque pra passar em Física III é se ater aos “grandes pontos”.
Resposta
a)
b)
c)