Introdução ao Campo Elétrico, Potencial Elétrico
Seja um anel carregado com uma densidade linear de carga em uma de suas metades e na outra, sendo uma constante, e seja o eixo de simetria perpendicular ao plano do anel.
Sabendo que o potencial elétrico no infinito é igual a zero, qual a única afirmativa verdadeira?
e sobre o eixo
e sobre o eixo
e sobre o eixo
e no centro do anel
e no centro do anel
Passo 1
Existem duas formas de resolver esse cara aqui: calculando o campo elétrico e o potencial no eixo (que dá mais trabalho), ou analisando a simetria do problema (que dá menos trabalho).
Sim, eu sei que você pensou o mesmo que eu... na prova talvez você perca um tempo que você não tem calculando e sobre o eixo , então vamos analisar a simetria do problema.
A ideia é mais ou menos essa:
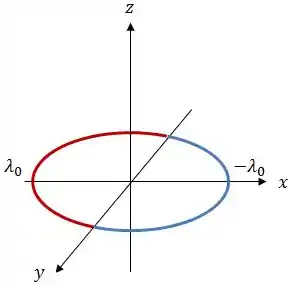
Vamos pegar dois pontos simétricos do anel, ambos com carga , e calcular o campo elétrico e o potencial resultantes em um ponto qualquer do eixo , beleza?
Passo 2
Analisando graficamente, o campo elétrico resultante entre esses dois pontos simétricos vai ser essa cara:
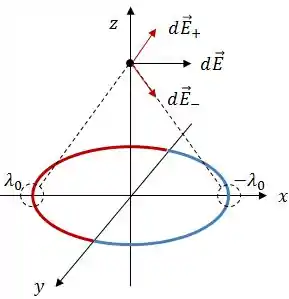
Inclusive, se pegarmos no ponto , vamos ver que esse cara também não se anula:
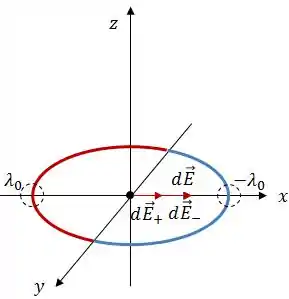
Isso vai acontecer para qualquer par de pontos simétricos, logo, podemos concluir que, tanto no eixo , quanto na origem:
Daqui já podemos descartar as opções , e .
Passo 3
Ok, agora vamos dar uma olhada no potencial elétrico, ok?
A ideia aqui é basicamente a mesma.
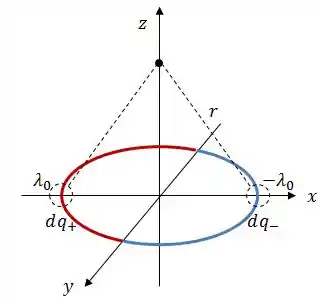
O potencial nesse ponto, que vamos chamar de , devido aos dois elementos de carga, será:
Onde e .
Portanto:
Isso vai acontecer para qualquer par de pontos simétricos, logo, podemos concluir que, tanto no eixo , quanto na origem:
Sendo assim, a resposta certa é a .
Resposta
e sobre o eixo