Um fio retilíneo fino, de comprimento , está postado ao longo do eixo cartesiano , com seu centro na origem desse. A densidade linear de carga de tal fio é dada por:

Onde .

1. Calcule o potencial eletrostático para um ponto arbitrário no eixo cartesiano , com ordenada . Faça, como usual, o potencial igual a zero no infinito [Sugestão: lembre-se que, para temos simplesmente ao passo que para temos ].
2. Calcule, agora, a componente do vetor campo elétrico em tal ponto;
3. Determine, por fim, a carga total de tal fio.

Trocando o diferencial das cargas pela fórmula da densidade:

O diferencial é pois o fio está ao longo de :

Substituindo:

Botando a densidade:

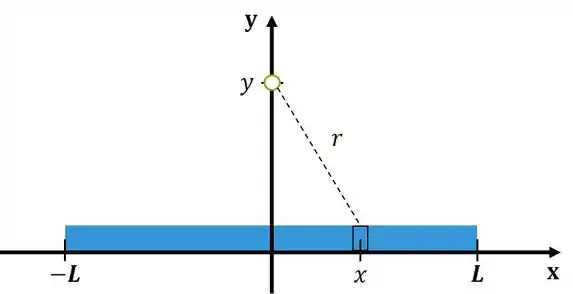
Pelo desenho tiramos que:

Analogamente tiramos os limites de integração:

Arrumando na vida:

Substituindo a fórmula da densidade:

Como estamos integrando no intervalo temos tanto negativo quanto positivo. Substituindo a definição do módulo de :

Arrumando mais:

A integral nós matamos com substituição simples:

Resolvemos a indefinida:

Então segue que:

Ufa. Portanto temos nosso potencial! Se você quiser substituir a constante , a resposta vai ficar:

Continuando, nós desejamos calcular a componente do campo elétrico. Dado que nós temos o potencial, achar o campo é moleza para fórmula abaixo:

Que é o operador de derivadas parciais. Portanto a componente vai ser o potencial derivado com relação a com sinal trocado:

Vê se não me esquece de trocar o sinal pfv! Partiu derivar:

Temos então:

Logo:

Se quiser substituir o valor de , a resposta fica:

Para obter a carga total basta integrar a densidade na barra toda:

Manipulando a função módulo: