Energia Potencial e Densidade de Energia, Potencial Elétrico
Há dois anéis com centros no mesmo eixo a uma distância um do outro e de raio também .
O anel possui carga uniformemente distribuída, e o anel 2 possui carga uniformemente distribuída.
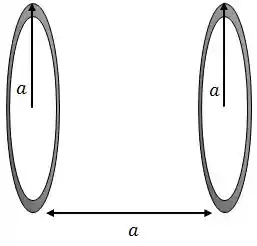
- Qual o potencial elétrico no centro de cada um dos anéis?
- Se colocarmos uma carga no centro do anel 1, qual o trabalho necessário que um agente externo deve realizar para leva-la até o centro do anel 2? (O sinal tem significado físico!)
Passo 1
a) Qual o potencial elétrico no centro de cada um dos anéis?
No centro de um dos anéis, o potencial resulta da soma dos potenciais dos dois anéis. Pra começar, vamos pegar o ponto no centro do anel da esquerda:
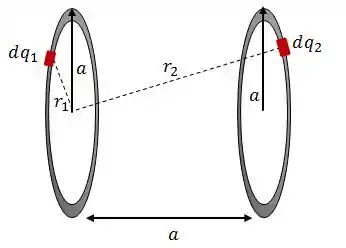
Cada elemento de carga gera um potencial elétrico . Logo:
Onde:
Por fim:
Já o potencial no anel da direita vai ter o mesmo raciocínio! É só trocar por !
Passo 2
b) Se colocarmos uma carga no centro do anel 1, qual o trabalho necessário que um agente externo deve realizar para levá-la até o centro do anel 2? (O sinal tem significado físico!)
Podemos associar a diferença de potencial com o trabalho a partir da relação:
Nesse caso é com sinal por que esse é o trabalho de uma força externa. Seria com sinal de se fosse o trabalho da força elétrica.
E a diferença de potencial é dada por
Assim
Substituindo os valores
Resposta
a.
b.