Uma camada semiesférica isolante de raio interno e externo tem uma densidade volumétrica de carga que decresce com o inverso da distância ao centro segundo .
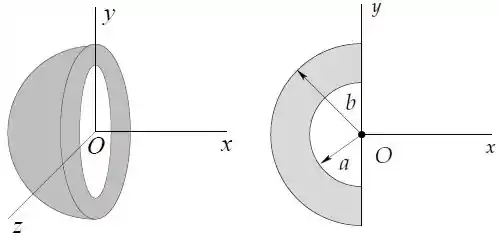
Dados e .
- Determine a carga total da camada semiesférica.
- Determine o potencial elétrico no ponto da cama semiesférica. Adote potencial nulo no infinito.
- Se uma carga pontual com o mesmo sinal da constante da densidade volumétrica de carga é solta no centro , qual é a velocidade final que ela atinge?
Passo 1
- Determine a carga total da camada semiesférica.
- Determine o potencial elétrico no ponto da cama semiesférica. Adote potencial nulo no infinito.
- Se uma carga pontual com o mesmo sinal da constante da densidade volumétrica de carga é solta no centro , qual é a velocidade final que ela atinge?
Beleza! O problema já nos dá a densidade volumétrica de carga
Por definição, a densidade volumétrica de carga é cada por:
Portanto, a carga total é dada por:
O elemento de volume é dado por
Onde é a área da semiesfera.
Lembrando que o raio varia entre e . Logo:
Por fim:
Passo 2
A definição de potencial elétrico diz que:
Como vimos no passo 1:
Substituindo na equação de :
Passo 3
Pra esse tipo de questão, o segredo é utilizar a conservação de energia.
Quando a carga está no ponto , ela possui energia potencial dada por:
Como já calculamos no item anterior, a energia potencial será:
No instante em que a carga é solta, ela possui apenas energia potencial, e não energia cinética.
Depois que a carga é solta, no infinito, toda essa energia potencial é transformada em energia cinética. Assim, de acordo com a conservação de energia, teremos: