Dois anéis finos concêntricos de raios e , encontram-se no plano . O centro dos anéis coincide com a origem do sistema de coordenadas, conforme a figura. O anel de raio possui carga total e o anel de raio possui carga total , ambas uniformemente distribuídas.
Calcule o potencial produzido por cada anel sobre o eixo .
Determine qual deve ser a carga no anel de raio para que ele produza no ponto do eixo , que está a uma distância da origem, o mesmo potencial eletrostático do anel de raio .
A partir do potencial, calcule o vetor campo elétrico em , em termos de e .
Passo 1
Calcule o potencial produzido por cada anel sobre o eixo .
Vamos começar calculando o potencial de um elemento de carga , que será dado por:
Onde é a distância entre o elemento de carga e um ponto no eixo . Mas se o eixo é o eixo de simetria do anel, você consegue ver que, para qualquer elemento do anel, a distância para um determinado ponto no eixo será sempre a mesma?
No caso do anel de raio :
Substituindo na expressão de , teremos:
Integrando dos dois lados, teremos o seguinte:
Para o anel de raio , o resultado será semelhante, as únicas diferenças são a carga do anel e o raio. Assim, o potencial do anel de raio será:
Passo 2
Determine qual deve ser a carga no anel de raio para que ele produza no ponto do eixo , que está a uma distância da origem, o mesmo potencial eletrostático do anel de raio .
O ponto fica a uma distância da origem. Além disso, o enunciado nos disse que .
Então a única coisa que temos que fazer é substituir esses valores e igualar e .
Logo de cara já podemos simplificar essa expressão:
Agora é só usar e .
Finalmente:
Passo 3
A partir do potencial, calcule o vetor campo elétrico em , em termos de e .
Bom, a primeira coisa aqui é explorar a geometria do problema. Pegando dois pontos opostos do mesmo anel, vamos ver o que acontece com o campo elétrico.
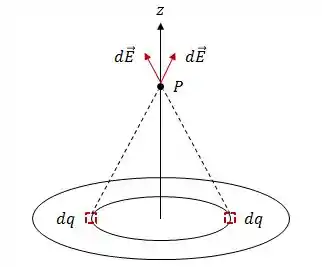
Consegue ver que as componentes perpendiculares ao eixo vão se anular e somente as componentes paralelas a vão se somar? Isso significa que o campo resultante estará apenas no eixo .
Por definição, o campo elétrico e o potencial elétrico estão relacionados por:
Onde o potencial resultante é a soma dos potenciais dos dois anéis:
Pra conseguirmos continuar trabalhando aqui, temos que usar as relações entre e e e .
Passo 4
Além disso, no ponto , .
Substituindo na expressão de , teremos:
Agora é manter a calma e ir arrumando a bagunça:
Como falamos no passo anterior:
Resposta