Um anel circular isolante está posicionado sobre o plano de um sistema de coordenadas, de forma que seu centro coincida com a origem. A situação é mostrada na figura abaixo.
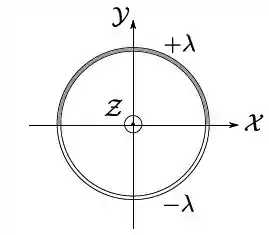
O anel possui uma densidade linear de carga constante em sua metade superior e em sua metade inferior . Utilizando o sistema de eixos da figura e tomando o potencial eletrostático como nulo no infinito, considere as afirmativas abaixo:
O potencial eletrostático é nulo em qualquer ponto sobre o eixo OZ.
O campo elétrico aponta no sentido negativo do eixo em qualquer ponto sobre o eixo .
O trabalho realizado pela força elétrica ao trazer uma partícula de carga do infinito ao centro do anel é positivo.
São VERDADEIRAS as afirmativas:
e
e
e
, e
Nenhuma delas.
Passo 1
Vamos analisar uma afirmativa por vez.
O potencial eletrostático é nulo em qualquer ponto sobre o eixo OZ.
Quando estamos trabalhando com anéis carregados, ou arcos de circunferência carregados, o potencial gerado é dado por:
Onde é a distância entre qualquer ponto do arco e qualquer ponto sobre o eixo .
Nesse caso, os dois arcos de circunferência possuem cargas iguais, mas de sinais diferentes, de modo que o potencial resultante em qualquer ponto sobre o eixo será:
A afirmativa é verdadeira.
Passo 2
O campo elétrico aponta no sentido negativo do eixo em qualquer ponto sobre o eixo .
Os campos gerados pelos arcos positivo e negativo terão essa cara:
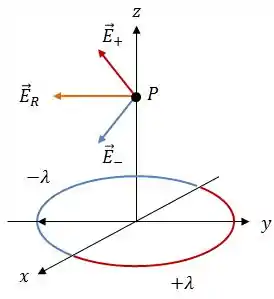
Como resultado, o campo apontará no sentido negativo do eixo . A afirmativa é verdadeira.
Passo 3
O trabalho realizado pela força elétrica ao trazer uma partícula de carga do infinito ao centro do anel é positivo.
Dado que o potencial elétrico no centro do anel é nulo, temos que, por definição:
No entanto, o potencial no infinito também é nulo, logo:
A afirmativa é falsa.
Resposta
e