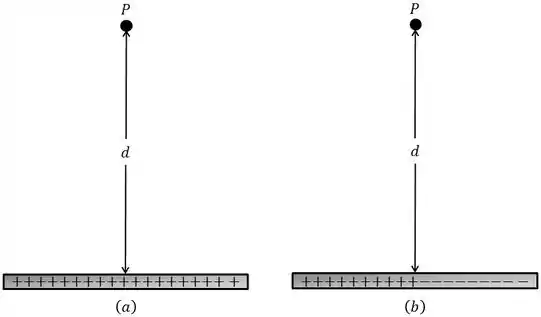
- A figura a seguir mostra uma barra não-condutora de comprimento e densidade linear de cargas positiva uniforme . Tome no infinito.
Qual é o valor de no ponto situado a uma distância acima do ponto médio da barra?
- A figura mostra uma barra idêntica à do item , exceto pelo fato de que a metade direta agora está carregada negativamente;
Qual é o valor de no ponto situado a uma distância acima do ponto médio da barra?
O valor absoluto da densidade linear de cargas continua a ser em toda a barra. Com no infinito, qual o valor de no ponto ?
Passo 1
- Qual é o valor de no ponto situado a uma distância acima do ponto médio da barra?
- Para a figura , qual o valor de no ponto ?
Como a barra é uniformemente carregada, o procedimento aqui consiste de pegar o potencial de uma carga pontual do corpo no ponto e integra-lo no corpo todo.
Como essa carga é infinitesimalmente pequena se comparada ao corpo, nós montamos a integral assim:
Passo 2
É sempre bom analisar graficamente isso para poder montar a integral corretamente.
A ideia é basicamente essa:
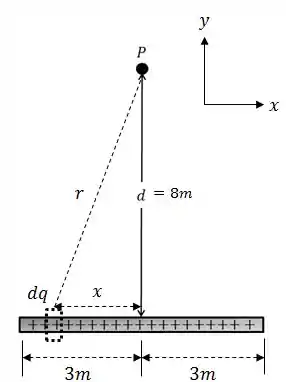
Daqui podemos tirar algumas conclusões... a primeira é que pode ser escrito como:
Outra coisa que podemos tirar daqui é: como a barra é uniformemente carregada, nós podemos usar a densidade linear de carga pra tentar facilitar a nossa vida:
Substituindo na expressão que encontramos para o potencial:
Basicamente, a questão sobre potencial já acabou, o problema agora é resolver essa integral escrota.
Vou colocar logo pra você a resposta dessa integral.
Onde:
;
;
;
Partiu!
Passo 3
Bom, antes de começar a esquentar a cabeça, vamos dar uma olhada na simetria do problema.
Como metade da barra é positiva e a outra metade é negativa, vamos pegar dois pontos simétricos em relação ao centro, com cargas de módulo , e ver como se comporta o potencial no ponto .
Graficamente, a ideia é basicamente essa
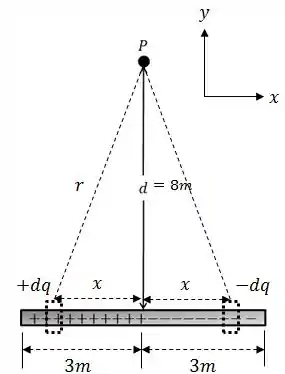
O potencial resultante desses dois elementos de carga, vai ser a soma dos dois potenciais. Portanto:
Eita! Se isso é verdade para quaisquer dois pontos simétricos, isso vai acontecer para toda a barra.
Portanto:
É razoável pensar também que, como as duas metades são iguais, mas com cargas de sinais opostos e como o potencial elétrico é uma grandeza escalar e não vetorial, as duas metades vão produzir o mesmo potencial, em módulo, no ponto , mas de sinais opostos.
Assim, quando for somar as duas, o resultado vai ser nulo.
Resposta
- ;
- ;