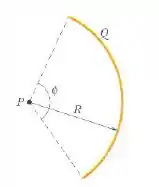
Uma barra de plástico com uma carga uniformemente distribuída tem a forma de um arco de circunferência de raio e um ângulo central . Com no infinito, qual é o potencial elétrico no ponto , o centro de curvatura da barra?
Passo 1
Escrever a contribuição infinitesimal de cada ponto do arco de circunferência para o potencial elétrico no ponto
Passo 2
Integrar as contribuições do passo anterior.
Note que o ângulo não foi importante na determinação do resultado.
Resposta
Exercícios de Livros Relacionados
Uma barra de plástico tem a forma de um circunferência de raio R = 8,20 cm. A barra possui uma carga Q 1 = +4,20 pC uniformemente distribuída ao longo de um quarto de circunferência e uma carga Q 2 =
A Fig. abaixo mostra uma barra fina de plástico que coincide com o eixo x. A barra tem um comprimento L = 12,0 cm e uma carga positiva uniforme Q = 56,1 fC uniformemente distribuída. Com V= 0 no infin
O rosto sorridente da Fig. Abaixo é formado por três elementos: 1: Uma barra fina com uma carga de -3,0μ C e a forma de uma circunferência completa com 6,0c m de raio; 2: Uma segunda barra fina com um
Qual é o módulo do campo elétrico no ponto 3,00 i ^ - 2,00 j ^ + 4,00 k ^ m se o potencial elétrico é dado por V = 2 x y z 2 , em que V está em volts e x, y e z estão em metros?
Um elétron é colocado no plano xy, onde o potencial elétrico varia com x e y de acordo com os gráficos da figura abaixo (o potencial não depende de z) . Em termos dos vetores unitários, qual é a força