Considere um plano infinito , uniformemente carregado, coincidente com o plano de um dado sistema de coordenadas. Sobre esse sistema, considere as afirmativas abaixo:
- Pode-se tomar o potencial elétrico como nulo sobre todos os pontos do plano .
- Qualquer plano paralelo à é uma superfície equipotencial.
- A diferença de potencial elétrico entre os pontos de coordenadas e é nula.
São VERDADEIRAS as seguintes afirmativas:
- e
- e
- e
- e
- Nenhuma delas.
Passo 1
Um plano infinito tem simetria planar e, por essa razão, o campo elétrico produzido pelo plano é sempre perpendicular ao plano e é constante, tendo o mesmo valor acima ou abaixo do plano. Para nos lembrarmos dessas características, vamos considerar que o plano tem carga positiva com distribuição superficial de carga , como está na figura abaixo.
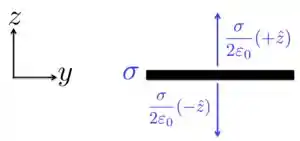
Como a carga é positiva, o campo elétrico que ela produz, acima ou abaixo do plano , tem módulo e aponta na direção e sentido de acima do plano e na direção e sentido de abaixo dele. Como o campo elétrico está relacionado ao potencial através de
o potencial acima do plano será dado por
e o potencial abaixo do plano será
Agora, vamos analisar cada item separadamente...
Passo 2
Como o potencial é linear com a distância , podemos tomar como nosso ponto de referência para o potencial, que é mais adequado nesse caso, já que no infinito temos (já que no passo anterior é menor que zero tanto pra quanto para ).
Por isso, o item está CORRETO.
Além disso, todos os pontos de planos paralelos ao plano à mesma altura dele (abaixo ou acima de ) terão o mesmo potencial, já que o potencial, como vimos no Passo 1, depende da posição ao plano com
O item está CORRETO.
Passo 3
Para fechar, para analisar a diferença de potencial, temos que tomar cuidado! Vamos tomar pontos acima do plano () com coordenadas e abaixo com coordenadas .
Para esse caso, o que temos que fazer é o seguinte:
Nós fizemos aqui para uma carga positiva , mas teríamos as mesmas conclusões para os itens da questão caso tivéssemos uma carga negativa. Por isso, as conclusões que tiramos são gerais para esse caso de um plano infinito carregado.
Assim, o item também está CORRETO.
Resposta
Letra d.