A figura abaixo representa um disco não condutor com um furo central com raios e . O disco está carregado com densidade superficial de carga .
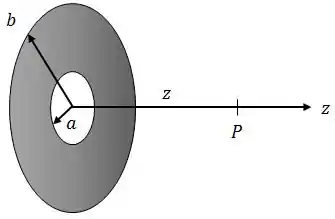
- Calcule o potencial elétrico no ponto , a uma distância do disco situado sobre o seu eixo central;
- A partir do potencial encontrado no item , calcule o vetor campo elétrico no ponto ;
- Fazendo simultaneamente e tendendo para infinito , que vetor campo elétrico resulta?
Passo 1
- Calcule o potencial elétrico no ponto , a uma distância do disco situado sobre o seu eixo central;
- A partir do potencial encontrado no item , calcule o vetor campo elétrico no ponto ;
- Fazendo simultaneamente e tendendo para infinito , que vetor campo elétrico resulta?
Vamos começar imaginando um anel de carga e raio que produz o seguinte potencial elétrico no ponto , a uma distância do anel.
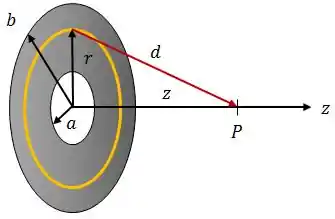
Onde . Logo:
Nós podemos associar a carga com a densidade superficial de carga através da relação:
Onde é a área do anel.
Logo, substituindo de volta na fórmula.
Agora é só integrar esse cara, onde :
Esse cara aqui é resolvido por substituição simples, chamando e . O resultado disso será:
Passo 2
Por definição, podemos associar o campo elétrico com o potencial elétrico através da relação:
Logo:
O vetor campo elétrico, nesse caso, vai sempre apontar no sentido do eixo , logo:
Passo 3
A expressão do campo elétrico que achamos ali em cima foi:
Quando e :
Que corresponde ao campo elétrico formado por uma placa infinita.
Resposta
a.
b.
c.