Dois anéis finos concêntricos de raios e , encontram-se no plano . O centro dos anéis coincide com a origem do sistema de coordenadas, conforme a figura. O anel de raio possui carga total e o anel de raio possui carga total , ambas uniformemente distribuídas.
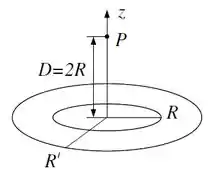
(a) Calcule o potencial produzido por cada anel ao longo do eixo , como função de .
(b) A partir do potencial, calcule a componente do campo elétrico em , em termos de e . Quanto valem as componentes e do campo elétrico? Justifique.
(c) Determine qual deve ser a carga no anel de raio para que ele produza no ponto do eixo , que está a uma distância da origem, o mesmo potencial eletrostático do anel de raio .
Passo 1
a) A distância de qualquer elemento de carga do anel de raio até o eixo vai ser a mesma, então a gente pode escrever que
Substituindo a distância :
Pra calcular o potencial do anel de raio , o procedimento é o mesmo, obtendo
Passo 2
b) Vamos perceber antes de qualquer coisa que por simetria, as componentes e do campo elétrico são nulas. Agora vamos calcular a componente .
Lembrando que . Logo:
Passo 3
c) Vamos igualar os potenciais obtidos na letra (a):
Resposta
O campo em e é nulo por simetria.