Um anel circular isolante de raio possui uma carga uniformemente distribuída sobre seu comprimento. Uma partícula de carga e massa encontra-se inicialmente em repouso sobre o eixo do anel, em um ponto muito afastado de seu centro. Desprezando a ação da gravidade, os módulos da velocidade e da aceleração dessa partícula quando ela passa pelo centro do anel valem, respectivamente:
(a) e
(b) e
(c) e
(d) e
(e) e
Passo 1
Para calcular a velocidade com que partícula chega ao centro do anel podemos usar conservação de energia
Quando a partícula está super afastada, a energia de interação entre o anel e a partícula é nula. Como a partícula parte do repouso, temos também que a sua energia cinética é nula, assim
Por outro lado, a energia da partícula no centro do anel é dada por
onde o primeiro termo é a sua energia cinética e é a energia de interação entre o anel e a partícula. Assim
Passo 2
Agora precisamos calcular a energia de interação entre a partícula e o anel.
Como o anel tem carga total e raio a densidade linear de carga do anel é dada por
Guarda isso aí que a gente vai usar mais tarde.
Cada pedacinho do anel, então terá um comprimento e uma carga de forma que
Como estamos falando de um anel, temos que em coordenadas polares o comprimento é dado por , ou seja
Cada pedacinho desse anel produzirá um potencial no centro do anel. Como o centro do anel está a uma distância do centro do anel, temos que
Substituindo o infinitésimo de carga, , podemos finalmente integrar em !
Substituindo
Agora que sabemos o potencial no centro do anel, podemos calcular a energia potencial da partícula no centro do anel
E assim podemos finalmente calcular a velocidade da partícula
Passo 3
No centro do anel temos que o campo elétrico é nulo. Isso por que para cada pedaço do anel com carga criando um campo no centro do anel haverá um outro pedaço do lado oposto do anel gerando um campo no centro do anel de mesma intensidade, porém no sentido oposto, conforme a figura
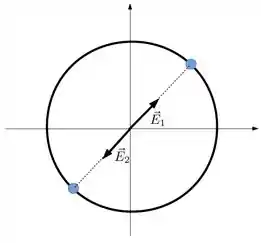
Assim, o campo elétrico no centro do anel será nulo e consequentemente a força elétrica sobre a partícula será nula também. Isso significa que sua aceleração no centro do anel é nula.
Resposta
(a)