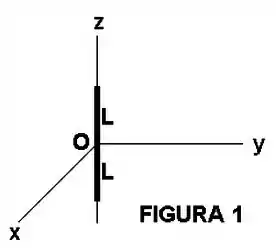
Um fio de comprimento está carregado uniformemente com a densidade linear de carga . Determine uma expressão para o potencial elétrico em um ponto arbitrário do eixo , conforme mostra a Figura .
Adapte a solução do item para determinar o potencial elétrico devido a um fio quadrado de lado , carregado uniformemente com a densidade linear de carga , em um ponto de observação arbitrário do eixo , conforme mostra a Figura .
Sugestão: calcule a distância entre o ponto de observação e o ponto médio de um dos lados do quadrado.
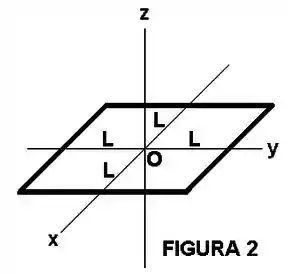
Determine o vetor campo elétrico devido ao fio quadrado no mesmo ponto de observação.
Passo 1
Bom, para resolver esse item, temos que aplicar a fórmula, pegamos o potencial de um ponto de carga e comprimento e achamos seu potencial num ponto arbitrário no eixo
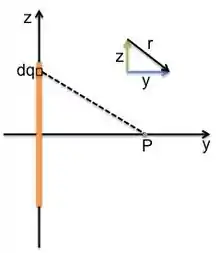
E vamos integrar em toda a barra para achar o potencial para o ponto arbitrário de :
Agora vamos brincar com essas variáveis para conseguir fazer a integral. O trocamos por um diferencial de espaço usando a equação da densidade:
O nós expressamos em termos das outras paradas usando o Pitágoras mesmo, se liga no triangulo desenhado na figura:
Partiu então:
O resultado da integral é:
Calma, esse resultado não saiu do bolso, essa integral é dada na capa da prova...Valeu, Cremona!
Passo 2
Para determinar o potencial em um ponto arbitrário do eixo , adaptando do que achamos no item , faremos algumas analogias, vamos começar pensando em apenas um dos lados do quadrado.
Ao invés de , como no item , a distância entre o meio da barra e o ponto arbitrário no eixo será:
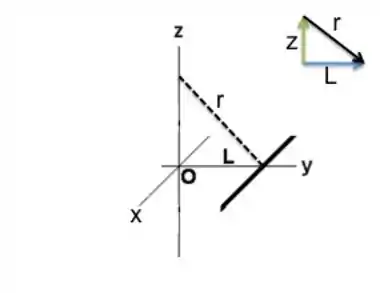
É isso que temos que substituir no lugar de na equação do potencial que achamos no item !
Substituindo, fica:
Agora sabemos o potencial gerado por um dos lados do quadrado, portanto, para os quatro, temos:
Passo 3
Como já sabemos o potencial, para determinar o módulo campo elétrico, devemos usar a seguinte fórmula:
Vamos derivar essa bagaça! Sem as constante antes, temos que a derivada do dá:
Simplificando:
Até que ficou bonitinho...plugando as constantes, temos que o campo é: