Densidade de Carga, Energia Potencial e Densidade de Energia, Potencial Elétrico
Considere um anel não-condutor situado no plano de raio interno e raio externo com uma densidade superficial de carga uniforme , como pode ser observado na figura.
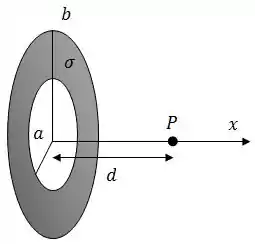
Calcule o potencial elétrico gerado por esta distribuição no ponto , a uma distância sobre o eixo indicado na figura.
A partir do resultado do item , encontre o campo elétrico (modulo, direção e sentido) no ponto .
Calcule o trabalho realizado para trazer uma carga puntiforme do infinito até o ponto .
Passo 1
Calcule o potencial elétrico gerado por esta distribuição no ponto , a uma distância sobre o eixo indicado na figura.
Vamos começar considerando um potencial gerado por um pedaço infinitesimal do disco de carga , de forma que:
Assim, o potencial será dado por:
Pra diferenciar a distância ao ponto e o raio do disco, vamos chamar o raio do disco de , beleza?
Continuando...
A áera do disco é dada por , logo, .
Graficamente, a ideia é essa:
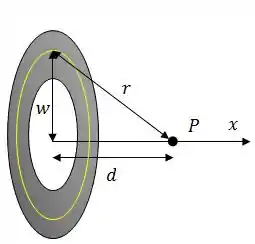
Onde:
Substituindo de volta na expressão de :
Passo 2
Pra finalizar, só temos que integrar esse cara em relação a , onde :
Essa é uma integral que não é difícil de resolver, mas que você não precisa se preocupar, porque a resposta dela provavelmente vai estar no seu formulário, então é só dar uma olhada.
Substituindo os limites de integração:
Passo 3
A partir do resultado do item , encontre o campo elétrico (modulo, direção e sentido) no ponto .
Antes de começarmos a pensar nas contas, vamos dar uma olhada na geometria do problema... pegando dois pontos equidistantes do ponto , vamos ver o que acontece com o campo elétrico.
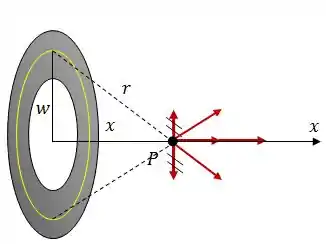
Como podemos ver, campo elétrico vai sempre se cancelar na direção paralela ao plano do disco, isso significa que temos apenas campo elétrico no sentido .
Utilizando o resultado da letra , o potencial elétrico em um ponto a uma distância do disco é:
Por definição:
Portanto:
Finalmente, o campo elétrico em um ponto a uma distância do disco é:
No ponto , , logo:
Passo 4
Calcule o trabalho realizado para trazer uma carga puntiforme do infinito até o ponto .
Essa é a mais tranquila... por definição:
No infinito . Portanto:
Substituindo a expressão de que encontramos na letra :
Resposta