Um anel circular fino de raio está uniformemente carregado com uma densidade linear de carga . Uma barra fina, de comprimento igual ao raio do anel e uniformemente carregada com a mesma densidade é posicionada inicialmente ao longo do eixo , que é perpendicular ao plano do anel e passa por seu centro, como mostrado na Figura à esquerda abaixo. A barra é posicionada de forma que uma de suas extremidades coincida com o centro do anel, como indicado na figura.
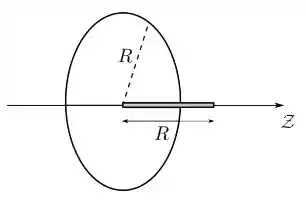
- Determine o potencial eletrostático produzido apenas pelo anel em um ponto sobre o eixo , localizado a uma distância do centro do anel. Considere que o potencial é nulo no infinito.
- Determine o campo eletrostático (módulo, direção e sentido) produzido apenas pelo anel no mesmo ponto .
- Determine a energia potencial eletrostática associada à interação entre o anel e a barra. Considere que a energia é nula quando o anel e a barra estão infinitamente afastados um do outro. Sugestão: Divida a barra em elementos de carga infinitesimais e considere a contribuição da interação entre este elemento e o anel para a energia total.
- Determine o trabalho realizado pela força eletrostática ao fazermos a barra atravessar completamente o anel, colocando-a em uma nova configuração onde sua extremidade oposta coincide com o centro do anel, como mostrado na figura abaixo. Justifique sua resposta.
Formulário:
Passo 1
a) Para calcular o potencial produzido pelo anel em um ponto à distância do centro do anel, considere a Figura abaixo.
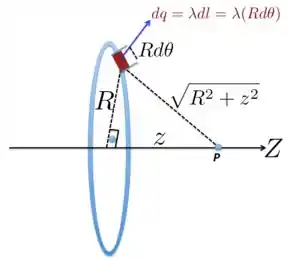
O elemento de carga está a uma distância fixa do ponto . Portanto, como , o potencial produzido em será
Como tanto quanto são independentes do ângulo , podemos integrar da seguinte maneira
Repara nessa equação que se a gente troca por , temos
Vamos usar esse resultado daqui a pouco.
Passo 2
b) Para analisar o campo elétrico, dá uma olhada na Figura abaixo. Nela, mostramos um elemento de carga e na outra ponta da reta tracejada ao longo do diâmetro outra carga idêntica . Eles são idênticos porque o enunciado diz que a distribuição linear é uniforme.
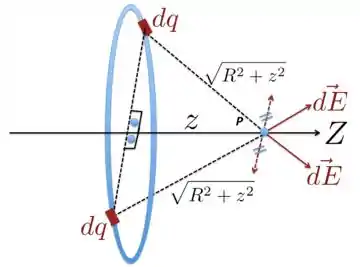
Identificamos também o campo elétrico que cada uma produz.No caso, esse campos têm o mesmo módulo . Por isso, as suas componentes paralelas à reta tracejada ligando as cargas se cancelam, sobrando apenas uma componente ao longo do eixo de simetria do anel, que está em .
A gente pode fazer o mesmo para todos os outros pares de cargas e chegaremos à conclusão de que o campo total produzido pelo anel no ponto está ao longo do eixo .
Sabendo disso, poderíamos encontrar esse campo elétrico total por integração. Mas não precisamos fazer isso, já que temos o potencial calculado no item anterior e porque sabemos também da seguinte relação:
Então, basta derivarmos o potencial com relação à variável para encontrarmos .
Então a derivada fica
Pela regra da cadeia:
E o campo fica
Fazendo isso, chegamos a:
Passo 3
c) Como a questão sugere, vamos tomar a energia associada a uma carga da barra na presença de um potencial criado pela distribuição de cargas do anel. Isso vai nos dar o seguinte
Substituindo o potencial que a gente tem do item a) e integrando, chegamos a
em que usamos a integral dada no formulário da prova.
Simplificando um pouco mais, temos
que é a energia associada ao sistema quando a barra está à direita do anel carregado.
Repara que a energia associada à barra quando ela está na posição à esquerda do centro do anel carregado é igual, pois , ou seja, poderíamos repetir toda a conta acima para a barra à esquerda e obteríamos que
Passo 4
d) Como o trabalho é , então o trabalho realizado para colocar a barra na segunda posição à esquerda do anela é