Uma coroa circular está uniformemente carregada com densidade superficial de carga , onde . A coroa possui raio interno , raio externo e está localizada no plano com o seu centro na origem, como mostrado na figura abaixo.
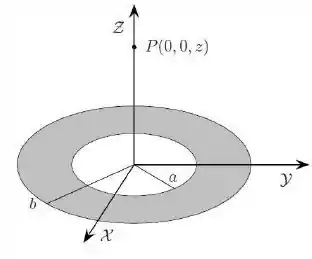
Determine a carga total da coroa.
Determine a expressão para o potencial eletrostático gerado por essa coroa circular no ponto , localizado no semieixo positivo .
Determine o campo elétrico (módulo, direção e sentido) gerado por essa coroa circular no ponto , localizado no semieixo positivo .
Formulário
Passo 1
Determine a carga total da coroa.
Como a carga está uniformemente distribuída na coroa circular, podemos dizer que:
Onde corresponde à área da coroa. Logo:
Passo 2
Determine a expressão para o potencial eletrostático gerado por essa coroa circular no ponto , localizado no semieixo positivo .
O segredo pra esse tipo de problema é começar olhando para o potencial gerado por um pedaço infinitesimal da coroa, com carga .
Nesse caso, dada a simetria do problema, vamos tratar desse pedaço infinitesimal como se fosse um anel com raio genérico , tal que , se liga:
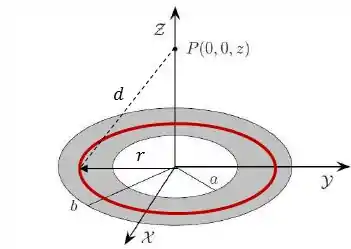
O potencial gerado por esse anel no ponto é dado por:
Onde .
Além disso, a carga infinitesimal está associada à densidade superficial de carga da seguinte forma:
Onde corresponde à área infinitesimal do anel.
Assim, substituindo e na expressão do potencial, teremos:
Passo 3
Pra fechar, basta integrar a expressão acima, onde :
Tirando o que não depende de da integral:
A resposta dessa integral consta no formulário da prova, então lá vai uma boa dica: toda vez que você vir uma integral que ache um pouco estranha, dê uma olhada no formulário, é possível que a resposta dessa integral esteja lá.
Continuando...
Passo 4
Determine o campo elétrico (módulo, direção e sentido) gerado por essa coroa circular no ponto , localizado no semieixo positivo .
Poderíamos usar o mesmo princípio que utilizamos pra calcular o potencial no item anterior, mas como já temos uma expressão do potencial, dada a simetria do problema, o campo terá apenas uma componente em , então podemos usar a seguinte relação:
Derivando a equação entre parênteses, teremos:
Arrumando a casa:
Resposta