![]()
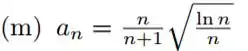
Passo 1
Bom, a gente sempre deve fazer o teste da divergência antes de tentar qualquer outro teste (a não ser que a série envolve um fatorial ou seja muito complicado de calcular o limite), porque se o cara for divergente, a gente já mata a questão, ok? Você lembra o que diz o teste da divergência?
Relaxa, nada mais é que calcular o limite do termo geral da série, quando . Se esse limite for diferente de zero, a série diverge, e se ele for igual a zero, nada podemos concluir. Então bora fazer esse teste:
Eita! Deu zero, então agora vamos para outro teste.
Passo 2
Olha nosso termo geral:
Estamos procurando uma série com um termo geral para calcularmos o limite:
Se esse for um número maior que zero, teremos que ou ambas divergem ou ambas convergem. Então vamos em busca desse .
Você vai escolher esse cara da seguinte forma:
Perceba que esse é o termo geral de uma série divergente! Vamos usar esse fato mais tarde.
Passo 3
Agora a gente calcula o limite:
Aparentemente, isso parece não dizer nada, mas tenho uma coisa pra te contar: quando esse limite do teste vai pra infinito e a série que você está comparando é divergente, isso significa que a sua série é divergente também.
Resposta
A série diverge.