UFSCAR – Séries e Equações Diferenciais – Simulado 10 – Questão 4
Em relação à série , tem-se que:
- A série:
Passo 1
Oi pessoal, tudo bem? Vamos começar?
O problema nos deu uma série e pediu duas coisas
- Na letra (a) pediu o limite do termo geral (termo geral é a expressão que está dentro do somatório, no nosso caso ) quando : aqui não tem muito mistério, tem que ter memória mesmo! Lembrar lá de cálculo 1! É só calcular o limite mesmo, usando todas as regrinhas que você já viu
- E na letra (b) perguntou se a série diverge ou converge. Aqui precisamos achar qual teste vai confirmar o comportamento dessa série, e aqui que entra o truque sujo! Mas calma, vou te ajudar a identificar qual teste usar!
Vamos fazer passo a passo juntos?
Vamos lá!
Passo 2
Letra (a)
Lembrando que é um número inteiro e positivo.
A função tem esse comportamento aqui:
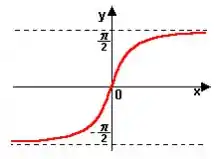
Para valores positivos de , a função tende a e para valores negativos, para . Como estamos fazendo o limite em , vamos olhar apenas para valores inteiros e positivos.
Assim, como nosso admite apenas valores positivos,
E embaixo? Bom embaixo temos , e quando , .
Assim o limite no infinito de :
Assim
Beleza?
E já vou fazer uma observação que vai servir para ver a convergência ou divergência de uma série: se o limite no infinito do termo geral dessa sequência for:
Sendo assim, como o limite da nossa série foi zero, ela pode convergir ou divergir. Isso significa que precisamos aplicar algum teste.
Passo 3
Agora vamos para letra (b).
Nossa série é
Como ela envolve uma função limitada em cima por , então isso sugere que podemos usar o teste da comparação
Vamos comparar a nossa série com uma outra que sabemos o comportamento, ou seja, comparamos nossa série com uma série conhecida.
E daí podemos ter duas opções:
- Sempre que a série conhecida estiver por cima “por cima” e convergir, então a nossa série (que está “por baixo”) também irá convergir
-
Sempre que a série conhecida estiver “por baixo” e divergir, então nossa série (“que está por cima”) também irá divergir
Passo 4
Uma série conhecida é a série harmônica:
E ela diverge! Então se ela estiver por baixo da nossa série, isso indica que nossa série vai divergir também.
Temos que a função arco tangente para valores positivos de :
Então podemos comparar nossa série com a série harmônica:
Sendo assim, se a série harmônica diverge, a nossa série também diverge!
Então a série é: divergente
Beleza? Espero ter ajudado!
Até a próxima!