2. Calcule a integral de superfície para o campo vetorial e superfície orientada . Em outras palavras, determine o fluxo de através de . Para superfícies fechadas, use a orientação (para fora) positiva.
c) , é a parte da esfera no primeiro octante com orientação para a origem.
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nessa questão temos uma integral de superfície em um caso vetorial!
Temos que determinar o fluxo dado por através de , onde e é a parte da esfera que está contida no primeiro octante e orientada para a origem.
Tem ideia de como podemos resolver essa questão?? 🤔🤔
Esses casos são obtidos usando uma formulinha dada por
O que temos que fazer é parametrizar , calcular seu vetor normal , aplicar a parametrização em , obter os limites de integração e calcular a integral.
Parece simples? Vamos começar? 😁
Passo 2
Primeiro vamos parametrizar a superfície . Como é uma esfera, podemos lembrar das coordenadas esféricas onde fazíamos as seguintes mudanças
Com sendo o raio da esfera.
Como nossa esfera foi dada e podemos ver que seu raio é , já que
Logo temos a seguinte parametrização
Ou também
Derivando com relação a , a e calculando o produto vetorial entre eles, vamos obter o vetor normal .
Primeiro derivamos com relação a
Lembrando do teorema fundamental do cálculo temos que as derivadas do e
Faremos o mesmo com relação a
Pelo teorema fundamental do cálculo, temos
Tudo bem até aqui? 👀
Passo 3
Agora vamos calcular o vetor normal a obtendo o produto vetorial de .
Calculando esse determinante, temos que
Se colocarmos em evidencia no último termo, temos
Sabemos que , logo podemos simplificar
Agora vamos aplicar nossa parametrização em
Transformando para
Calculando o produto interno entre e , temos
Calculando o produto de cada termo ( com , com ...) e somando-os
Está acompanhando? 😉
Passo 4
No enunciado, foi dito que estamos interessados em , no primeiro octante
Lembrando das coordenadas esféricas
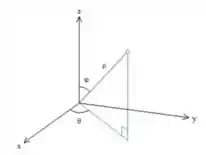
Quais os valores para e descrevem a parte de uma esfera dentro do primeiro octante?
Para , a variação que pode ser feita é de a , até porque menos ou mais que isso, caímos em outros octantes.
Da mesma forma para , o primeiro octante está contido entre .
Com isso, definimos os limites para e para como
Com essas informações podemos montar nossa integral como
Ficou enorme, não é? Mas relaxa, vamos com calma.
Vamos separar a integral da soma pela soma da integral
Calculamos as integrais e e somamos os resultados.
Primeiro vamos resolver a integral
Vamos integrar com relação a , então o que não conter pode sair da integral
Podemos reescrever como . Mas o que é ? Podemos reescreve-lo como
Dessa forma, nossa nova integral é
Assim podemos aplicar o método de integração por substituição fazendo , com isso
Entendeu essa parte? 🤔
Passo 5
Portanto, nossa integral será
Tirando o sinal para fora e aplicando o método de integração polinomial, temos
Substituindo por de volta
Aplicando os limites de integração
Logo a primeira integral é
Agora com base nesse resultado, integramos com relação a
Aplicando identidades trigonométricas, temos
Separando essa integral, temos
Pelo método de substituição sendo e
Pelo teorema fundamenta do cálculo, temos
Substituindo por de volta, finalmente, temos
Ta achando tranquilo? 👀
Passo 6
Aplicando os limites de integração no resultado anterior, temos
Enfim, temos nossa primeira integral
Agora vamos para a segunda integral! A integral
Primeiro integrando com relação a , podemos escrever nossa integral como
Vamos aplicar o método de substituição fazendo como e como
Aplicando o método de integração polinomial, temos
Voltando para
Aplicando os limites de integração
Ao pouquinho vamos chegando lá!
Passo 7
Integrando o resultado anterior com relação a , temos
Pelo teorema fundamental do cálculo, temos
Aplicando os limites de integração
Assim conseguimos mais um resultado
Como obtemos os resultados de e vamos soma-los para obter a resposta final
Deu um trabalhinho né? Mas obtemos que o fluxo pela nossa região é !
É isso! Essa resolução te ajudou? Responde Aí! ✌
