Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial

Ver Teoria
Exercício 8312345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182

Enunciado

UTFPR, Londrina, Cálculo 3, Provas de C3 - Prof Marcele Tavares - AV1 - 2023.1, Questão 1.iii

Explicite duas estratégias para calcular ∬ s F d s , onde F x , y , z = ( y z 2 , x z 2 , x 2 + y 2 ) e S é a superfície definida por z = x 2 + y 2 tal que 0 ≤ z ≤ 1 .

Passo 1

Antes de pensarmos em qualquer estratégia, vamos visualizar a superfície S com o nosso querido GeoGebra.

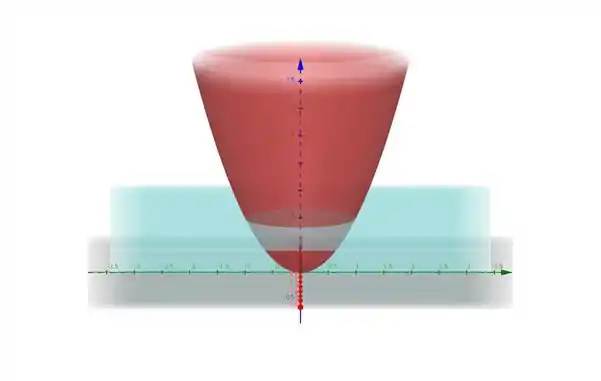
Passo 2

Estratégia 1: Uso de coordenadas cartesianas

Uma maneira de calcular a integral é usar coordenadas cartesianas. Isso envolve parametrizando a superfície S e então usando a definição da integral de superfície para calcular a integral. A parametrização da superfície S é dada por

x = u cos ⁡ v

y = u sin ⁡ v

z = u 2

onde 0 ≤ u ≤ 1   e   0 ≤ v ≤ 2 π .

Passo 3

Estratégia 2: Uso de coordenadas polares

Outra maneira de calcular a integral é usar coordenadas polares. Isso envolve parametrizando a superfície S e então usando a definição da integral de superfície para calcular a integral. A parametrização da superficie S é dada por

x = r cos ⁡ θ

y = r sin ⁡ θ

z = r 2

Onde 0 ≤ r ≤ 1   e   0 ≤ θ ≤ 2 π .

Resposta

Ver o desenvolvimento.

Exercícios de Livros Relacionados

Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
A temperatura de um ponto da bola com condutividade K é inversamente proporcional à distância do centro da bola. Determine a taxa de transmissão de calor através de uma esfera S de raio a e centro da
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por y = h ( x , z ) e n → é o vetor normal unitário que aponta para a esquerda.
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por x = h ( y , z ) e n → é o vetor normal unitário que aponta para frente (ou seja, para o observador, qua