Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial

Ver Teoria
Exercício 5012345678910111213141516171819202122232425262728293031323334353637383940414243444546474849515253545556575859606162636465666768697071727374757677787980818283

Enunciado

Tarefa 2, Grau G2 - MAT 1163 Cálculo III – PUCRIO – Questão 2

Considere a região elíptica R e o semi-elipsóide S do exercício 1. Considere também os campos

G → x , y , z = 1 2 - y i ^ + x j ^ e H → x , y , z = k ^

a) Assumindo que os vetores normais à R   e S tem componentes k ^ positivas, calcule

∫ ∫ R H → ⋅ n → d A e ∫ ∫ S H → ⋅ n → d A

b) Denote por C a elipse R   ∩   S . Orientando C de forma que o vetor tangente t em ( 1 ,   0 ,   0 ) tenha componente j ^ positiva, calcule

∫ C G ⋅ t d l

Passo 1

a) Vamos começar calculando primeiramente a integral abaixo...

∫ ∫ R H → ⋅ n → d A

A gente sabe que a região R é dada por...

x 2 + y 2 4 ≤ 1 ,   z = 0

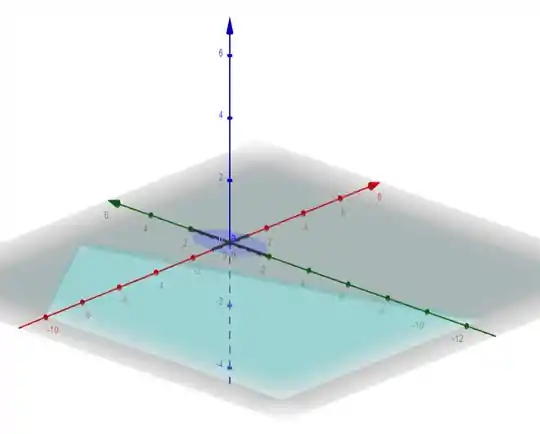
Bem! Temos a elipse abaixo...

x 2 + y 2 4 = 1

Bora dar um jeito de parametrizar ela...

x = cos ⁡ θ

y = 2 sen ⁡ θ

z = z

Logo;

φ θ , z = ( cos ⁡ θ , 2 sen ⁡ θ , z )

Agora, vamos encontrar o vetor normal à superfície...

∂ φ ∂ θ = ( - sen ⁡ θ , 2 cos ⁡ θ , 0 )

∂ φ ∂ z = ( 0,0 , 1 )

∂ φ ∂ θ × ∂ φ ∂ z = i ^ j ^ k ^ - sen ⁡ θ 2 cos ⁡ θ 0 0 0 1 = ( 2 cos ⁡ θ , sen ⁡ θ , θ )

E como podemos ver, a normal tem sinal positivo apontando para fora da superfície, conforme fala o enunciado... Só que por z valer zero, nem vale a pena calcular essa integral pois ela vai valer zero...

∫ ∫ R H → ⋅ n → d A = 0

Passo 2

Quanto à outra integral...

∫ ∫ S H → ⋅ n → d A

Como já vimos, temos o seguinte gráfico para essa superfície

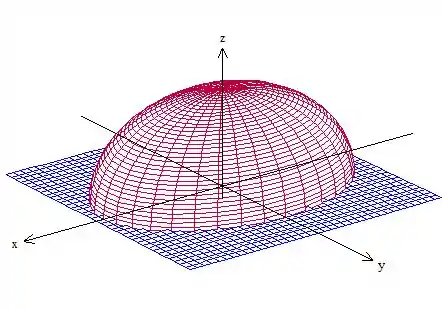
Onde S é essa casca do elipsoide cortada pelo plano x y . Pelo Teorema de Gauss, podemos escrever o seguinte

∬ ∂ W   G → d s = ∭ w   d i v G →   d V

Ou seja, a integral de superfície de uma função G sobre uma superfície fechada é igual à integral tripla do divergente dessa função no sólido limitado por essa superfície. Aplicando isso ao problema, podemos pensar que G = r o t ( F ) e que a casca do elipsoide S , junto com a elipse contida no plano x y E , formam uma região fechada.

Assim, escrevemos:

∬ S r o t ( F ) ∙ d S + ∬ E r o t ( F ) ∙ d S = ∭ w   d i v r o t ( F )   d V

Como o que queremos é o primeiro termo dessa expressão:

J = ∭ w   d i v r o t F   d V - ∬ E r o t ( F ) ∙ d S

Passo 3

Vamos começar pela integral tripla. Vamos calcular o rotacional de F . Temos:

F x , y , z = ( x z ,   y z ,   x y )

r o t F → = ∇ ×   F → = i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z F 1 F 2 F 3

r o t F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

r o t F → = x - y ,   x - y ,   0 - 0

r o t F → = x - y ,   x - y ,   0

O divergente do rotacional é, então:

d i v r o t   F = ∂ F 1 ∂ x +   ∂ F 2 ∂ y + ∂ F 3 ∂ z

d i v r o t   F = 1 - 1 + 0 = 0

Portanto, temos:

∭ w   d i v r o t F   d V = 0

Passo 4

Beleza, agora vamos calcular a integral de superfície.

∬ E   r o t   F .   d S = ∬ D   r o t F → . ∂ φ ∂ x × ∂ φ ∂ y d x d y

Primeiro, vamos parametrizar nossa nova superfície E e calcular seu vetor normal. Como a elipse está contida no plano x y , podemos parametrizá-la como:

φ x , y = ( x , y , 0 )

Onde os parâmetros x e y devem estar “dentro” da projeção da superfície no plano x y , ou seja, dentro da elipse.

Fazendo a interseção do elipsoide x 2 4 + y 2 + z 2 = 1 com o plano z = 0 , temos:

x 2 4 + y 2 = 1

Como queremos os pontos que estão dentro da elipse, temos:

x 2 4 + y 2 ≤ 1

Passo 5

Esse é o domínio da superfície E . Agora vamos calcular a normal dessa superfície.

∂ φ ∂ x = ( 1,0 , 0 )

∂ φ ∂ y = ( 0,1 , 0 )

∂ φ ∂ x × ∂ φ ∂ y = i j k 1 0 0 0 1 0 = ( 0,0 , 1 )

Como o problema diz que os vetores normais apontam para fora no elipsoide (ou seja, para cima), para manter o sentido vetorial correto, eles devem apontar para cima no plano. Como o vetor que encontramos possui a coordenada z positiva, quer dizer que ele está no sentido correto!

Passo 6

Escrevendo o rotacional em termos das variáveis da parametrização, temos:

r o t F → = x - y ,   x - y ,   0

x = x

y = y

z = 0

r o t F → = x - y ,   x - y ,   0

Legal, deu no mesmo!

Ok, vamos continuar.

Passo 7

Agora, vamos montar a integral de superfície

∬ E   r o t   F .   d S = ∬ D   x - y ,   x - y ,   0 . ( 0,0 , 1 ) d x d y

Onde D é dado por

x 2 4 + y 2 ≤ 1

O domínio da parametrização. Vamos calcular isso aí então:

∬ D   0   d x d y = 0

Olha que maravilha, nem precisamos fazer mais conta : )

Passo 8

Assim, temos o seguinte:

J = ∭ w   d i v r o t F   d V - ∬ E r o t ( F ) ∙ d S

J = 0 - 0

Resposta

a)

0 e 0

b)

π

Exercícios de Livros Relacionados

Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
A temperatura de um ponto da bola com condutividade K é inversamente proporcional à distância do centro da bola. Determine a taxa de transmissão de calor através de uma esfera S de raio a e centro da
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por y = h ( x , z ) e n → é o vetor normal unitário que aponta para a esquerda.
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por x = h ( y , z ) e n → é o vetor normal unitário que aponta para frente (ou seja, para o observador, qua