Considere o campo vetorial
Calcule a integral onde o campo é definido e é a superfície composta pelo cilindro , cortado por cima pelo plano , e completada por baixo pelo paraboloide , formando desta maneira um “copo”, com fundo parabólico e a parte lateral cilíndrica, deixando aberta a parte de cima. Sendo apontando para fora do “copo”.
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
O problema nos pede para calcularmos uma integral da superfície. Como eu faço isso?
Geralmente integrais de superfície são calculadas da seguinte forma: começamos parametrizando a superfície, e uma vez que essa superfície é parametrizada, temos que ver como a nossa função reage a essa superfície, certo? Então aplicamos a parametrização na função. Ah... Fica mais fácil mostrando essa parte e explicando o restante:
Nós explicamos a parte do . Mas o que é depois? Bom o produto vetorial é devido ao sentido em que aponta, pois sendo uma superfície, precisamos saber para onde o fluxo aponta. Dessa forma:
E essa região aí? Ora, ela é a nova superfície parametrizada. “Basicamente” é isso. Fazer que é o difícil, né?! Ksksk mas confiante, vamos detonar essa questão!
Agora que já temos a faca e o queijo na mão, vamos ao lanche?
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Então ok, temos que parametrizar o sistema, certo?! Mas qual parametrização? Bom, nós temos duas superfícies aqui: uma parabólica e uma cilíndrica. De forma que temos que parametrizar ambas. Por qual prefere começar? Eu vou começar pela cilíndrica, mas pode começar pela parabólica, como quiser.
Bom, então temos uma superfície cilíndrica, logo podemos usar a coordenadas cilíndricas na nossa parametrização.
Mas como elas são:
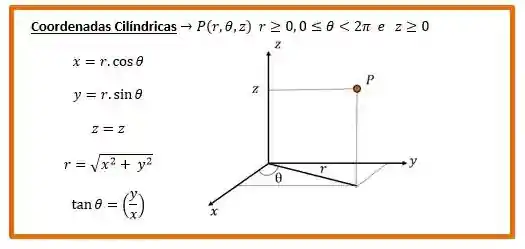
Bom, podemos ver que o passo mais importante é determinar o raio da coordenada cilíndrica. Ela é dada por:
Mas o que temos como e ? Ora, temos na nossa função
A coordenadas é e é . Então:
Mas essa expressão é familiar, né? Nas nossas equações, nós temos:
Então temos que . Até aqui ok, agora vamos achar as coordenadas e
Na parametrização cilíndrica
Onde
Assim nossa parametrização é:
Agora vamos para o paraboloide? O paraboloide deve ter ciúmes do cilindro, porque ele não tem uma coordenada própria hashua, ele é basicamente mesmo. Assim:
Então achamos ambas, vamos agora aplicar à elas?
Passo 3
Podemos seguir a ordem e começar aplicando às parametrizações cilíndricas? Assim, lembrando que :
E para o paraboloide, lembrando que :
Próximo passo agora é acharmos as derivadas parciais das nossas parametrizações.
Passo 4
Então temos que achar e para a parametrização cilíndrica, e e . Vamos começar pela cilíndrica?
E:
Agora vamos fazer do paraboloide?
E:
Agora que achamos as derivadas, temos todo o material pra nossa integral
Passo 5
Assim:
Melhor fazemos uma de cada vez, né?! Afinal vão ser um pouco grandes
Passo 6
Para a primeira:
temos
Substituindo , e
Podemos começar fazendo o produto vetorial. Assim:
Assim:
Agora fazendo o produto escalar:
E agora o ultimo passo é achar os limites de integração. Já determinamos anteriormente no passo 2 que . Mas e ?
Sabemos que , mas lembra das nossas formulas do cilindro e da limitação do plano que nos foi dado?
Mas sabemos que , assim:
E esse é o limite superior onde o plano corta o cilindro. E o inferior? O inferior é dado por que vem da equação . Assim a nossa integral fica
E agora basta integrando. Integrando em :
Integrando em :
Resumindo:
Agora vamos pra segunda integral?
Passo 7
Para a segunda integral:
Temos:
Substituindo e :
Podemos começar fazendo o produto vetorial:
Substituindo então:
Fazendo o produto escalar:
Assim a nossa integral fica:
Agora temos que definir os limites de integração. Mas não precisamos fazer isso para e , podemos passar para coordenadas polares. O que acha?
Assim:
Já obtivemos antes isso, né?
Logo:
Onde e o jacobiano é . E quais são os limites de ? vai de 0 e sobe até que é como determinamos antes. Assim:
Integrando em :
Integrando em :
Resumindo
Agora temos tudo que precisamos.
Passo 8
Então tínhamos:
Agora substituindo os valores:
EEEE UFAAAAA, ACABAMOS.
E acabamos por aqui, carinha. Obrigado por ter vindo até aqui comigo.