Questão 1:
b) Calcule
Sendo a parte do plano limitada pelo paraboloide , orientada com a normal unitária de modo que .
Passo 1
Antes de qualquer coisa, vamos primeiro melhorar a notação para termos uma clara noção do que fazermos. A integral de superfície no caso vetorial que queremos
pode ser reescrita de uma forma bem mais elegante como sendo...
Onde o campo é no nosso caso...
O bom dessa notação é só que assim fica mais fácil de seguir o passo a passo de resolução de integrais de superfície no caso vetorial:
1º - Parametrizar a superfície .
2º - Substituir os termos da parametrização na função vetorial .
3º - Encontrar o termo .
Bora lá?
Passo 2
Devemos parametrizar a superfície , mas por falar nisso quem é ela? Seria muito bom se tivéssemos uma visão mais geométrica dela.
Tenha em mente bem fixo que a superfície é o plano ...
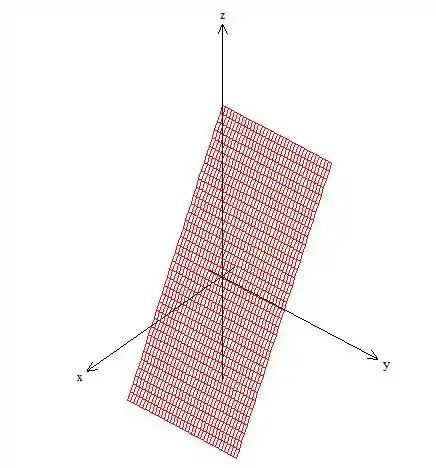
Só que delimitado pelo paraboloide ...
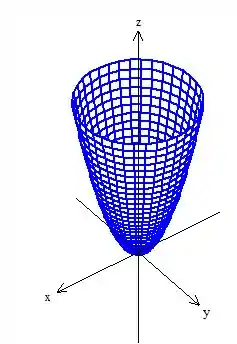
Sendo assim, eis a superfície ...
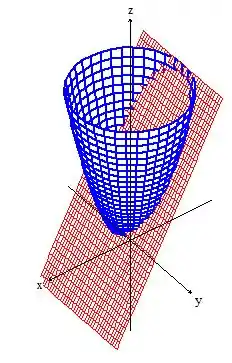
Passo 3
Para parametrizar, como a superfície é um pedaço de um plano, podemos pensar em uma parametrização explícita, onde e continuam os mesmos (no caso os parâmetros) e o do plano, vira...
Então a parametrização que encontramos de uma forma mais elegante é...
Passo 4
Nunca devemos sair de uma parametrização sem antes determinarmos onde os parâmetros (no caso e ) estão variando.
Bem, se você reparar novamente o esboço geométrico dele...
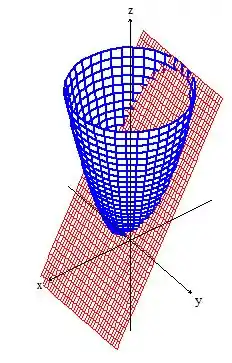
Vai perceber que a superfície plana está sendo delimitada pelo encontro com o paraboloide. Esse encontro em matemática é a solução do sistema com a equação de ambas as superfícies:
Isolando em cima e substituindo...
Completando quadrado já que ...
Eis que essa equação nos representa uma elipse
E essa elipse e justamente a região onde os parâmetros e variam. Por hora, para não perdermos o foco na resolução da integral de superfície, basta falar que . Depois se precisar, descrevemos em coordenadas elípticas ;)
Passo 5
Pelo passo a passo legal do passo , é hora de substituir os parâmetros da parametrização:
Na função que estamos integrando:
Ou seja...
Repare que como o campo tem como componente , e , quando trocar pela parametrização, coincidentemente dá a mesma parametrização
Passo 6
Para encontrar o termo ...
Onde o vetor normal, usualmente pode ser determinado por, calculando:
Calculando essas derivadas parciais...
Calculando a outra derivada parcial...
Voltando para o produto vetorial lembrando que esse é dado pelo cálculo de um determinante:
Então
Passo 7
Agora, aqui sempre devemos nos perguntar: estamos com o vetor correto? Ou temos que inverter o sinal dele?
Para responder a essa pergunta, basta verificar a condição de orientação que o problema nos disse, o que no caso é
Como o vetor ...
Logo, estamos lidando com o vetor correto, percebeu? Se tivesse dado negativo, bastava multiplicar todas as entradas do vetor normal por ;)
Então o termo
Passo 8
Voltando à integral que queremos resolver...
E trocando todos os termos que encontramos em cada passo...
Observe que trocamos o por , afinal agora vamos calcular uma integral dupla em e necessitando do domínio deles, sacou? Calculando o produto escalar
Agora é só calcular a integral dupla e correr para o abraço!
Passo 9
Olha que maneiro, a integral de um é a área da região que nesse caso é a elipse...
Uma área de elipse é dada por...
Onde e vem da equação geral de uma elipse...
Não esquenta com e , pois eles representam a coordenada do centro da elipse. No nosso caso, já vimos no passo que...
Então o e dando a área de...
Como...